The Covalent Bond Classification Method:

A New Approach to the Formal Classification of
Covalent Compounds of the Elements

 

Malcolm L. H. Green

J. Organomet. Chem. 1995, 500, 127-148.

 

Introduction

Covalent molecules are often described in terms of the oxidation state formalism in which a charge is assigned to the atom of interest.  While the oxidation state concept has proven to be of use in the traditional coordination chemistry with simple ligands, e.g. Cl– and NH3, it has become evident that this concept is of limited utility in organometallic and modern coordination chemistry because of the more complex nature of the ligands involved.  For example, the cycloheptatrienyl (C7H7) ligand has been assigned charges of +1, –1, and –3; as such, it is evident that the oxidation state of the metal has little meaning in complexes with such ligands.  In this regard, a recent IUPAC article concludes that it is inappropriate to assign oxidation numbers with respect to the nomenclature of organometallic compounds, viz: “As oxidation numbers cannot be assigned unambigously to many organometallic compounds, no formal oxidation numbers will be attributed to the central atoms in the following section on organometallic nomenclature.” 1999, 71, 1557-1585).

 

Also criticizing the use of oxidation states, Seddon and Seddon have written:  “…the oxidation state concept can be thought of as the Dewey Decimal Classification of inorganic chemistry – if the rules are applied, a number is obtained”.  But Seddon and Seddon continue: “Does oxidation state have a chemical significance?  A number is always obtained – does it mean anything?” (The Chemistry of Ruthenium, Seddon, E. A.; Seddon, K. R. Elsevier, New York, 1984; Chapter 2.)

 

In addition to problems associated with assignment of oxidation number, the assignment of “coordination number” is often ambiguous because the term is interpreted with more than one meaning in the literature.  For example, what is the coordination number of chromium in (h6‑C6H6)2Cr?  Common answers include 2, 6 and 12, depending on one’s notion of “coordination number”.

 

The problems associated with classifying molecules by oxidation number and coordination number stem from the application of a classification system to a set of molecules for which it is not appropriate.  In order to surmount problems of the types described above, Malcolm Green introduced an innovative method for the formal classification of covalent compounds (Green, M. L. H. J. Organomet. Chem. 1995, 500, 127-148).  The principal advantage of the so‑called “Covalent Bond Classification (CBC) Method” is that it was specifically designed for covalent molecules. 

 

In essence, the CBC method seeks to classify a molecule according to the nature of the ligands around the central element of interest.  The method is based on the notion that there are three basic types of interaction by which a ligand may bond to a metal center and the ligand is classified according to the nature and number of these interactions. 

 

The three basic types of interaction are represented by the symbols L, X, and Z, which correspond respectively to 2-electron, 1-electron and 0-electron neutral ligands and are clearly differentiated according to a molecular orbital representation of the bonding.

 

 

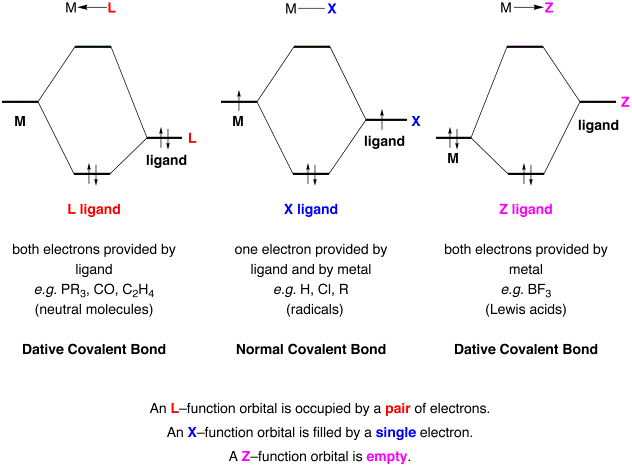
An L‑function ligand is one which interacts with a metal center via a dative covalent bond (i.e. a coordinate bond), in which both electrons are donated by the L ligand.  As such, an L‑function ligand donates two electrons to a metal center.  Since the metal uses no electrons in forming the M–L bond, an L‑function ligand does not influence the valence of a metal center.  Simple examples of L‑type ligands include R3P, R2O, and CO, i.e. donor molecules that have lone pairs (Lewis bases).

 

An X‑function ligand is one which interacts with a metal center via a normal 2‑electron covalent bond, composed of 1 electron from the metal and 1 electron from the X ligand.  As such, an X‑function ligand donates one electron to a metal center.  Since the metal uses one electron in forming the M–X bond, each X‑function ligand raises the valence of the metal center by one unit.  Simple examples of X‑type ligands include H and CH3, i.e. radicals.

 

A Z‑function ligand also interacts with a metal center via a dative covalent bond, but differs from the L‑function in that both electrons are donated by the metal rather than the ligand.  As such, a Z‑function ligand donates zero electrons to a metal center.  Since the metal uses two electrons in forming the M–Z bond, a Z‑function ligand raises the valence of the metal center by two units.  Simple examples of Z‑type ligands include BF3, BR3 and AlR3, i.e. molecules that have a vacant orbital (Lewis acids).

 

More important than merely referring to the number of electrons involved in the bonding is the fact that the types of interaction are differentiated according to the nature of the molecular orbital interaction (see above).  It is, therefore, apparent that the CBC method is of much more relevance to classifying and providing insight into the nature of covalent organometallic molecules than are methods based on (i) oxidation number (which merely hypothetically decomposes a molecule into its constituent ions) and (ii) electron count (that focuses only on the number of electrons, regardless of their origin).

 

A given ligand may have one or more of the above functions.  As such, the ligand may be classified as [XxZz], where l, x, and z are the respective number of L, X, and Z functionalities.  For example, the h6‑benzene ligand is classified as [L3], with the three L functionalities corresponding to the three “olefinic” moieties (see below).  Likewise, the h5‑cyclopentadienyl ligand is classified as [L2X], with the two L functionalities corresponding to the two “olefinic” fragments while the X functionality corresponds to the CH “radical” portion of the resonance structure. 

 

 

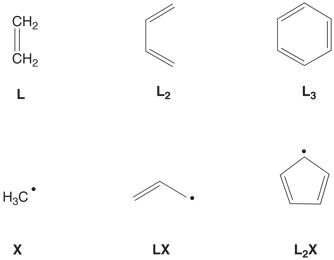
At a more fundamental level than merely relating to the number of electrons a ligand donates, however, the [LlXxZz] classification refers to the nature of the frontier orbitals of the neutral ligand, as illustrated for the Cn–symmetric CnHn ligands (see below). 

 

 

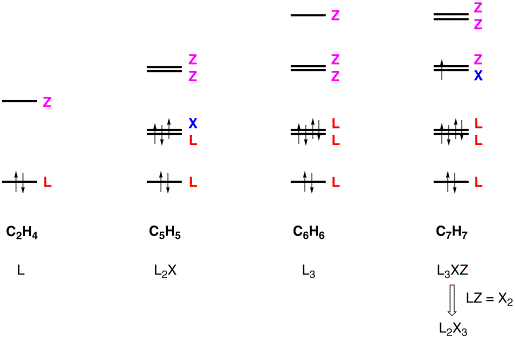
For example, the three highest energy occupied orbitals of the C5–symmetric C5H5 radical comprise a pair of doubly degenerate orbitals (HOMO) and a nondegenerate orbital (HOMO–1).  The HOMO–1 orbital is fully occupied and corresponds to an L function, while the HOMO is occupied by three electrons and corresponds to an L and an X function.  As such, C5H5 is classified as an [L2X] ligand.  The three highest energy occupied orbitals of C6H6 also comprise a pair of doubly degenerate orbitals (HOMO) and a nondegenerate orbital (HOMO–1), but since these are all occupied, C6H6 is classified as an L3 ligand.  An interesting situation arises, however, with C7–symmetric C7H7 because the HOMO is a singly occupied doubly degenerate orbital.  As such, the HOMO is an XZ combination.  Coupled with the L2 nature of the fully occupied doubly degenerate HOMO–1 orbital, and the L nature of the HOMO–2 orbital, the C7H7 ligand is classified as L3XZ; however, this classification reduces to L2X3 because an LZ combination is equivalent to that of an X2 combination.  In essence, one may view the valence state of the C7H7 ligand to have three unpaired electrons, in much the same way that carbon has a sp3 valence state with four unpaired electrons when it combines to form a tetrahedral compound.

 

The Equivalent Neutral Class

Once all the ligands about a metal center have been classified as described above, the molecule itself is classified as [MLlXxZz]Q± by summing all the L‑, X‑, and Z‑ functionalities, as illustrated below for some tungsten complexes. 

 

 

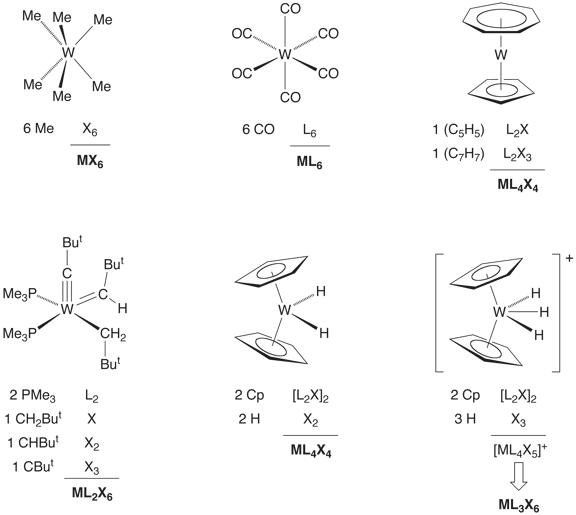
For example, Cp2WH2 is classifed as [ML4X4] since Cp  [L2X] and H  [X].  Correspondingly, [Cp2WH3]+ would be classified as [ML4X5]+.  However, in order to allow for comparisons between molecules that have different charges, it is useful to reduce the [MLlXxZz]Q± assignment to its “equivalent neutral class”, which is essentially the classification that would be obtained if the Q± charge were to be localized on the ligand and not on the metal center. 

 

For cations, the transformations are:  (i)  L+  X, i.e. a cationic 2‑electron donor is equivalent to a neutral 1‑electron donor, and (ii) X+  Z, i.e. a cationic 1‑electron ligand is equivalent to a neutral 0–electron ligand.  For anions, the most commonly encountered transformations are:  (i) X–  L, i.e. an anionic 1‑electron donor is equivalent to a neutral 2-electron donor and (ii)  L–  LX, i.e. an anionic 2‑electron donor is equivalent to a 3‑electron donor.  It is important to emphasize that the latter two transformations should be applied sequentially, i.e. a negative charge is only placed on an L–function if there is no X–function.  Finally, if the derived classification after performing the above transformations contains both an L and a Z function, the classification is reduced further by using the transformation LZ = X2.

 

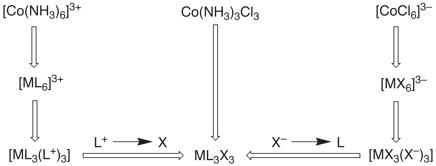
A consideration of some simple compounds serves to indicate the rationale for describing a molecule in terms of its equivalent neutral class.  For example, the cationic, neutral, and anionic octahedral Co(III) species [Co(NH3)6]3+, [Co(NH3)3Cl3], and [CoCl6]3_, which are related by the formal substitution of Cl– by NH3, each belong to the same fundamental molecular class, i.e. [ML3X3] (see below).  Thus, even though the compounds have different charges, the CBC method indicates that the three molecules belong to the same class of compound.

 

 

The [MLlXxZz] classification, electron number, valence and ligand bond number

Once the [MLlXxZz] classification of a molecule is known, it is a simple matter to extract other useful information pertaining to the nature of a molecule, including the electron count, valence, and ligand bond number (Table 1). 

 

Table 1.  Definitions pertaining to the CBC method.

 

Symbol

Definition

L

2–electron donor function

l

number of L functions

X

1–electron donor function

x

number of X functions

Z

0–electron donor function

z

number of Z functions

m

number of electrons on neutral metal

VN

valence number

VN = x + 2z

LBN

ligand bond number

l + x + z

EN

electron count

m + 2l + x

dn

number of electrons in “nonbonding” metal orbitals

n = m – x – 2z = m – VN

 

For example, the electron number (EN) of the metal in [MLlXxZz], i.e. the electron count, is given by EN = m + 2l + x, where m is the number of valence electrons on the neutral metal atom.

 

The valence number (VN) of the metal center, i.e. the number of electrons that the metal uses in bonding, is VN = x + 2z.  In most organotransition metal complexes, the number of Z ligands in the equivalent neutral class is zero.  As such, the valence number is typically equal to x, i.e. the number of one-electron donor X‑ligands.  The value of the dn configuration is given by n = m – x – 2z = m – VN. 

 

Finally, the ligand bond number (LBN) represents the effective total number of ligand functions surrounding M, and is defined as LBN = l + x + z.  While not defined as the coordination number, it is pertinent to note how the ligand bond number as defined by l + x + z gives the value that organometallic chemists “want” the coordination number to be in many compounds.  For example, both (h5–C5H5)2Cr and (h6–C6H6)2Cr (i.e. ML4X2 and ML6, respectively) have a ligand bond number of six, even though the classical definition of coordination number gives values of 10 and 12, respectively.  Furthermore, it is noteworthy that the ligand bond number reduces to the classical definition of coordination number when the ligands are “simple”, i.e. monofunctional ligands that coordinate to the metal using a single orbital, e.g. H and CH3.

 

MLX Plots

Since the [MLlXxZz] classification contains information that relates to the electron count, the valence and ligand bond number, it provides a greater dimension for classifying compounds than methods based on either electron count or oxidation number.  The [MLlXxZz] classification may be represented as a function of the electron count and valence number of the metal in diagrams are often simply referred to as “MLX plots”.  An illustration of an MLX plot is provided by the example for organometallic compounds of iron is shown below (data compiled by Cary Zachmanoglou from compounds listed in the Dictionary of Organometallic Compounds); MLX plots for other elements are presented at the end of this article.

 

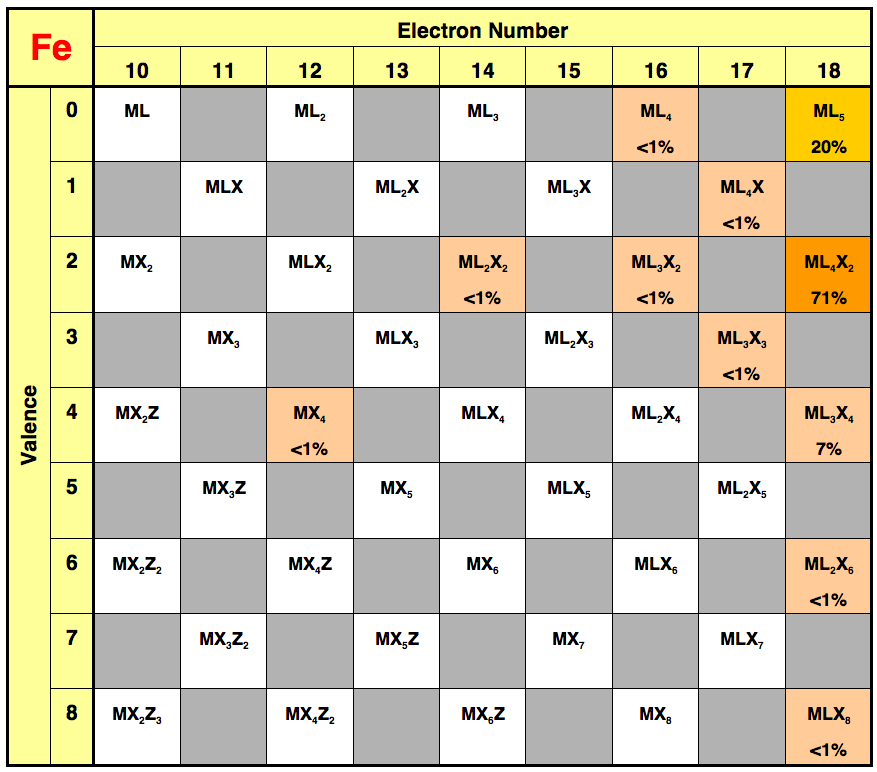
For example, while consideration of the electron count for iron compounds results in the conclusion that the organometallic chemistry of iron is dominated by 18–electron molecules, i.e. a single class of molecules, consideration of the MLX plot shows that this class of molecule can be further conveniently divided into additional classes.  Specifically, 18–electron iron complexes belong to [ML5], [ML4X2], and [ML3X4] classes, representatives of which are Fe(CO)5, Cp2Fe, and [CpFe(CO)(m–CO)]2.

 

MLX plots are a characteristic of each element and are provided at the end of this article for organometallic compounds of Groups 3 – 10 transition metals (Parkin, G. in Comprehensive Organometallic Chemistry III, Volume 1, Chapter 1; Crabtree, R. H. and Mingos, D. M. P. (Eds), Elsevier, Oxford, 2006).  In general, each element favors one or several [MLlXxZz] classes and the three most common for each element are summarized below. 

 

 

Group 3

Group 4

Group 5

Group 6

Group 7

Group 8

Group 9

Group 10

ScL4X3 (36%)

ScL5X3 (33%)

ScL3X3 (10%)

TiL4X4 (49%)

TiL5X3 (9%)

TiL2X4 (7%)

VL6X (22%)

VL4X4 (16%)

VL4X3 (14%)

CrL6 (48%)

CrL5X2 (24%)

CrL4X4 (7%)

MnL5X (79%)

MnL4X3 (12%)

MnL3X5 (1%)

FeL4X2 (69%)

FeL5 (20%)

FeL3X4 (7%)

CoL3X3 (54%)

CoL4X (34%)

CoL2X5 (4%)

NiL2X2 (33%)

NiL3X2 (26%)

NiL4 (16%)

YL5X3 (37%)

YL6X3 (22%)

YL4X3 (19%)

ZrL4X4 (55%)

ZrL5X4 (25%)

ZrL6X2 (6%)

NbL5X3 (32%)

NbL6X (17%)

NbL4X5 (15%)

MoL5X2 (40%)

MoL4X4 (25%)

MoL6 (19%)

TcL5X (75%)

TcL4X3 (14%)

TcL3X5 (2%)

RuL4X2 (79%)

RuL3X4 (9%)

RuL5 (8%)

RhL3X (41%)

RhL3X3 (27%)

RhL4X (22%)

PdL2X2 (81%)

PdL3X2 (9%)

PdL3 (4%)

LaL4X3 (31%)

LaL6X3 (22%)

LaL3X3 (17%)

HfL4X4 (58%)

HfL6X2 (11%)

HfL5X4 (8%)

TaL2X5 (23%)

TaL4X5 (15%)

TaL5X3 (14%)

WL5X2 (34%)

WL4X4 (27%)

WL6 (15%)

ReL5X (49%)

ReL4X3 (29%)

ReL3X5 (4%)

OsL4X2 (83%)

OsL5 (8%)

OsL3X4 (7%)

IrL3X3 (47%)

IrL3X (26%)

IrL4X (20%)

PtL2X2 (69%)

PtL2X4 (11%)

PtL3 (9%)

 

Trends elucidated from MLX plots

By summarizing a vast quantity of factual information, the MLX plot reveals important characteristics of the chemistry of the element under consideration and the information embodied in an MLX plot enables a variety of periodic trends to be established by comparing the distributions for the elements.

 

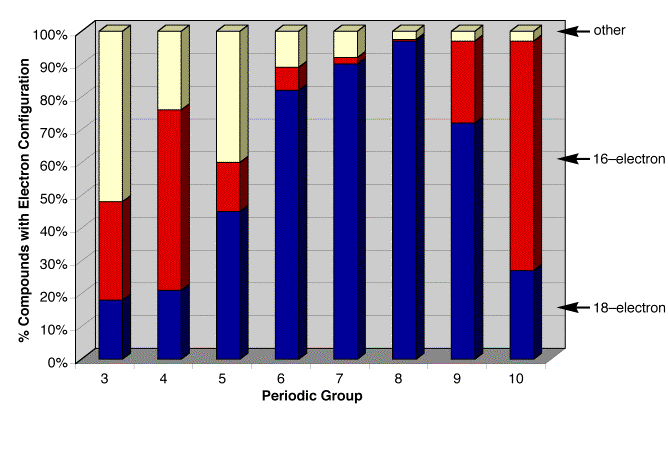
(i) Electron count

Since the electron count for a molecule of class [MLlXxZz] is given by EN = m + 2l + x, it is a simple matter to use the [MLlXxZz] classification to evaluate the distribution of molecules according to a specific electron count.  For example, the data indicate that  “18‑electron rule” is most closely obeyed for the middle portion of the transition series (Groups 6 – 8), as illustrated by the blue bars.  Both the earlier and later transition metals exhibit many deviations from this rule. 

 

(ii) Valence

With respect to the distribution of valence as a function of group, it is evident that the occurrence of the group valence is common up to Group 5, after which the two lowest valence states with an even dn configuration become prevalent (see below). 

 

 

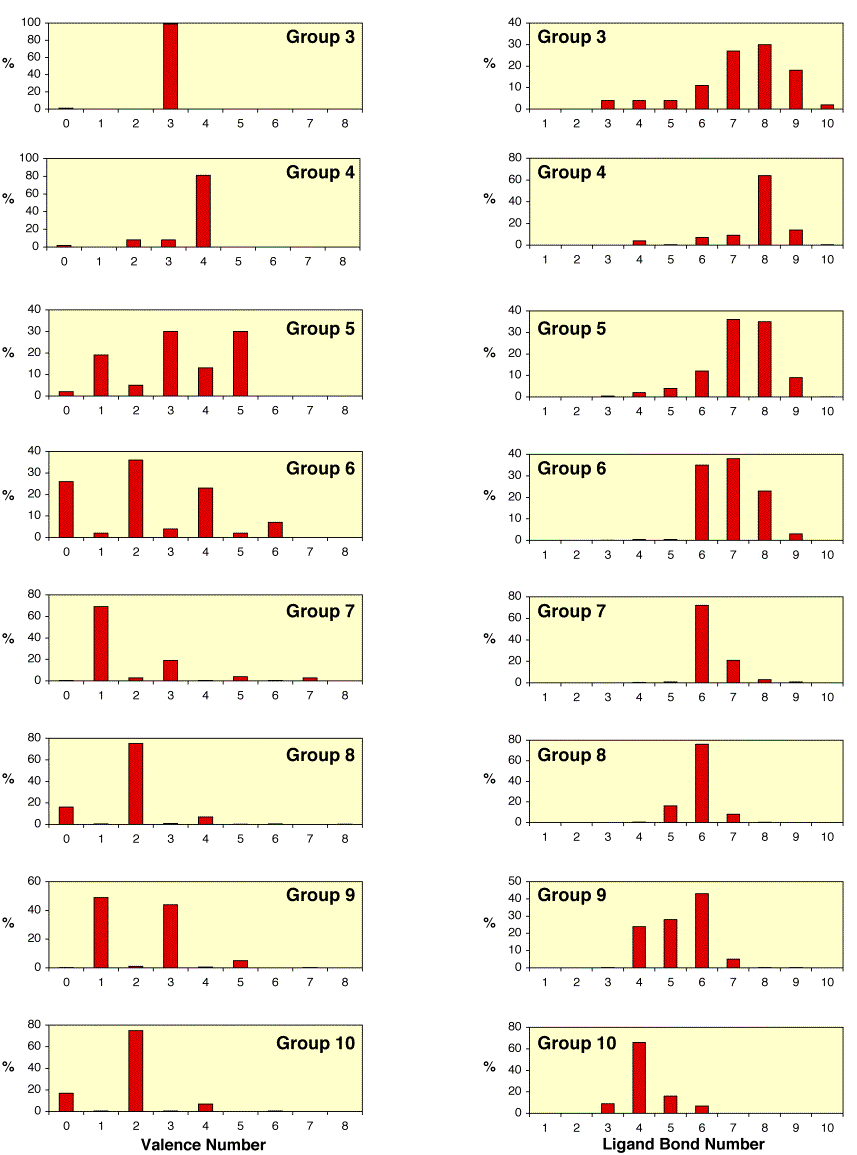
(iii)  Ligand bond number

The ligand bond number (cf. “coordination number”) decreases smoothly upon passing from Group 3 to Group 10 (see above).  Specifically, the most common ligand bond number decreases from 8 for Group 3 to a value of 4 for Group 10.

 

Summary

In summary, the CBC method is based on an elementary molecular orbital analysis of metal–ligand bonding interactions and a molecule is described in terms of the representation MLlXxZz where Ll, Xx and Zz refer to the number of 2–electron, 1–electron, and 0–electron donor functions.  By embodying the electron count (m + 2l + x), the valence of the metal (x + 2z), the ligand bond number (l + x + z), and the dn configuration (n = m – x – 2z), the MLlXxZz classification affords much more information than that provided by the oxidation number.  Furthermore, by identifying the different types of metal–ligand bonding interactions, the MLlXxZz classification describes the nature of the metal in the molecule of interest, while the oxidation number merely describes the charge on the metal after all ligands have been removed (!). Finally, since there are several different methods used to assign oxidation numbers, there is often ambiguity in the derived values.  These problems are exacerbated for organometallic compounds and, as such, the MLlXxZz classification provides a much more useful method of classification for these molecules.

 

MLX plots for organometallic compounds of the transition metals of Groups 3 – 10 and distributions of electron count, valence and ligand bond number are available here.  For further discussion of the CBC method, see:  Parkin, G. in Comprehensive Organometallic Chemistry III, Volume 1, Chapter 1; Crabtree, R. H. and Mingos, D. M. P. (Eds), Elsevier, Oxford, 2006.