Turbulent Flow: Ra = 6.75E+05

Introduction

Physically, the box is .15m high and .31m wide. Both side walls are adiabatic and the box is heated from below with a bottom wall temperature of 301K and a top wall temperature of 299K.The fluid is considered an ideal gas with appropriate reference properties assigned. A forty by eighty (3200 cell) mesh is used with a stretching factor of 1.5 in the x-direction.

HEAT FLUX: Expected vs. Actual-Expected heat flux: q = 2.15W/m^2 (According to the Nusselt number correlations obtained from experiments by Holland et al.(1975)). Actual heat flux: q=2.13W/m^2

Graphical Representations of Selected Results

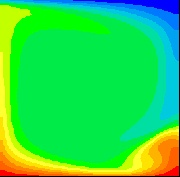
Temperature Field (K)

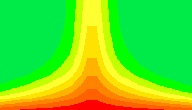
Velocity Profile (m/sec)

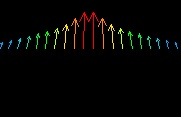
Velocity Field (m/sec)

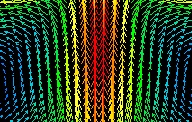
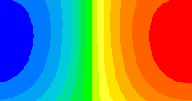Streamline Contour (m^2/sec)

Analysis:

All convergence factors comply more than satisfactorily. Even the heat flux values differ by only one one-hundredth of a Watt. In addition, while comparing the results published by J.W.Deardorff(1964) it is interesting to note that the temperature contours of the steady state solutions of this case using Pheonics 2.1, and the detailed pictures supplied by the author in his article, look remarkably similar. Given the unstable nature of this case, this is reassuring!

Again, as it is for case1, a pair of dominant vortices are formed within the rectangular region. However, unlike case1 the direction of air flow in the vortices is reversed. Hot air rises in the central region and cool air drops along the side walls. In addition, two eddies appear in the lower corners.

The maximum velocities for this case are about 5cm/sec. While comparing results of case1 with case2, it is interesting to note that although the Rayleigh number has increased by at least a magnitude of one hundred that the velocities have little more than doubled. This suggests a power relationship between maximum velocities and the Rayleigh number.