A digression into quirky statistics

Excerpt from the "Phantom Tollbooth" from Norton Juster (with illustration from Jules Feiffer)

Up he went - very quickly at first-then more slowly - then in a little while even more slowly than that - and finally, after many minutes of climbing up the endless stairway, one weary foot was barely able to follow the other. Milo suddenly realized that with all his effort he was no closer to the top than when he began, and not a great deal further from the bottom. But he struggled on for a while longer, until at last, completely exhausted, he collapsed onto one of the steps.

"I should have known it," he mumbled, resting his tired legs and filling his lungs with air. "This is just like the line that goes on forever, and I'll never get there."

"You wouldn't like it much anyway," someone replied gently. "Infinity is a dreadfully poor place. They can never manage to make ends meet."

Milo looked up, with his head still resting heavily in his hand; he was becoming quite accustomed to being addressed at the oddest times, in the oddest places, by the oddest people-and this time he was not at all disappointed. Standing next to him on the step was exactly one half of a small child who had been divided neatly from top to bottom.

"Pardon me for staring," said Milo, after he had been staring for some time, "but I've never seen half a child before."

"It's .58 to be precise," replied the child from the left side of his mouth (which happened to be the only side of his mouth).

"I beg your pardon?" said Milo.

"It's .58," he repeated; "it's a little bit more than a half."

"Have you always been that way?" asked Milo impatiently, for he felt that that was a needlessly fine distinction.

"My goodness, no," the child assured him. 'A few years ago I was just .42 and, believe me, that was terribly inconvenient."

"What is the rest of your family like?" said Milo, this time a bit more sympathetically.

"Oh, we're just the average family," he said thoughtfully; "mother, father, and 2.58 children and, as I explained, I'm the .58"

"It must be rather odd being only part of a person," Milo remarked.

"Not at all," said the child. "Every average family has 2.58 children, so I always have someone to play with.

Besides, each family also has an average of 1.3 automobiles, and since I'm the only one who can drive three tenths of a car, I get to use it all the time."

"But averages aren't real," objected Milo; "they're just imaginary."

"That may be so," he agreed, "but they're also very useful at times. For instance, if you didn't have any money at all, but you happened to be with four other people who had ten dollars apiece, then you'd each have an average of eight dollars. Isn't that right?"

"I guess so," said Milo weakly.

"Well, think how much better off you'd be, just because of averages," he explained convincingly. "And think of the poor farmer when it doesn't rain all year: if there wasn't an average yearly rainfall of 37 inches in this part of the country, all his crops would wither and die".

It all sounded terribly confusing to Milo, for he had always had trouble in school with just this subject.

"There are still other advantages," continued the child. "For instance, if one rat were cornered by nine cats, then, on the average, each cat would be 10 per cent rat and the rat would be 90 per cent cat. If you happened to be a rat, you can see how much nicer it would make things."

"But that can never be," said Milo, jumping to his feet.

"Don't be too sure," said the child patiently, "for one of the nicest things about mathematics, or anything else you might care to learn, is that many of the things which can never be, often are. You see," he went on, "it's very much like your trying to reach Infinity. You know that it's there, but you just don't know where but just because you can never reach it doesn't mean that it's not worth looking for."

"I hadn't thought of it that way," said Milo, starting down the stairs. "I think I'll go back now."

"A wise decision," the child agreed; "but try again someday perhaps you'll get much closer." And, as Milo waved good-by, he smiled warmly, which he usually did on the average of 47 times a day.

"Everyone here knows so much more than I do," thought Milo as he leaped from step to step.

The Mississippi flood of 1993

• The Mississippi River is the sixth largest river in the world in terms of discharge, with a freshwater discharge onto the continental shelf of 580 cubic km/yr.

• It is 2,320 miles long and drains 41 of the land area of the continental United States

History

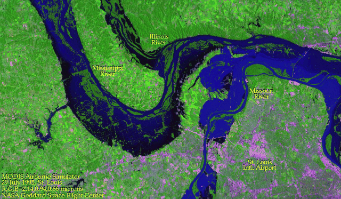
This Landsat image is centered on the Missouri River at Glasgow, near the St. Louis airport. At this location the Missouri River is flooding, due to the high level of the Mississippi.

• The flood of 1993 in the upper Mississippi River Basin was an unprecedented hydrometeorological event. In June and July (and somewhat into the fall) of that year, the Mississippi River basin in the midwestern United States experienced anomalously high rainfall which produced record flooding. The cause of the high precipitation was a persistent atmospheric weather pattern consisting of a quasi-stationary jet stream positioned over the central part of the nation. As a result, moist air flowing north from the Gulf of Mexico converged with unseasonably cool, dry air moving south from Canada.
• In June and July, close to 14 inches of precipitation (averaged over the upper Mississippi River Basin) was observed, significantly higher than average (approximately 8 inches).
• The fall of 1992 and spring of 1993 were already quite wet and the subsurface was saturated.
• At 45 USGS stations, the discharge rate exceeded the 100 years flood value (USGS streamflow gauges).

• The flood lasted for weeks!
• Estimates of total damages in the Midwest from weather events during 1993 ranged between $12 and $16 billion.
• Over half of these were agricultural damages, with the remaining being primarily to residences, businesses, public facilities, or transportation.
• 100,000 home were damaged, 50% of those due to groundwater or sewer backup.
• Thirty-eight deaths were attributed directly to the flood.
• Many levees broke, as evident in the satellite pictures

This Landsat image of the Mississippi River was taken in 1988.

This Landsat image of the Mississippi River was taken in 1993

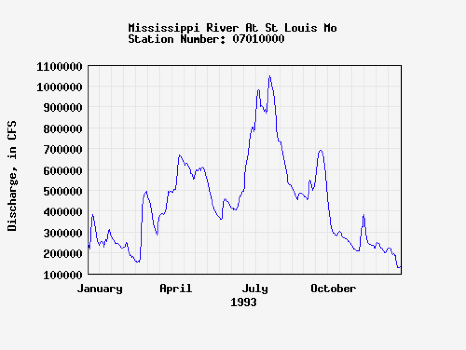
The Mississippi River at St. Louis, Missouri

• location of St. Louis in the upper Mississippi River Basin

• Click on links for examples of overall acreage damages and emergency costs and finally for a overall extent of flood. Feel free to consult the Army Corps of Engineer’s web site for more info.

Flood Prediction: The Mississippi case-study:

1) Upload the data annual peak discharge data of the Mississippi at St Louis (StLouis-Discharge). If you like, you can visit the source of the data on the USGS water resources page (Mississippi River At St Louis Mo).

2) Make a histogram of the entire data set and verify (visually) that it is normally distributed.

3) Calculate the natural logarithm of the annual peak discharge and determine the basic statistics of those data (MIN, MAX, AVERAGE, STDEV)

4) Calculate the discharge rate equivalent to the 100 years flood (P=0.01). (in Ft³/sec. Do not forget to reverse the transformation by using the EXP function):

a) Graphically: Transform the data by calculating exceedance level (r/(n+1)) and then plot that vs. lnQ. Use this graph to estimate the value of the 100 years flood. (Note: You can use 1) a regression function applied to the portion of the curve that is linear ob 2) a polynomial fitted to the entire data set).

b) Formula: Use the NORMINV function to determine this value. The NORMINV function in Excel returns the inverse of the normal cumulative distribution for the specified mean and standard deviation. Syntax: NORMINV(probability,mean,standard_dev), where “Probability” is a probability corresponding to the normal distribution, “Mean” is the arithmetic mean of the distribution, and “Standard_dev” is the standard deviation of the distribution.

c) Are these values similar? Explain why.

5) Do the same for the 1000 year flood

6) How does the 1993 flood compare to these two discharge rates (100- and 1000-years floods)?

7) What is the recurrence interval of the 1993 flood at St. Louis? Use the NORMDIST function. The NORMDIST function in Excel returns the normal distribution for the specified mean and standard deviation. Syntax: NORMDIST(x,mean,standard_dev,cumulative), where “X” is the value for which you want the distribution, “Mean” is the arithmetic mean of the distribution, “Standard_dev” is the standard deviation of the distribution, and “Cumulative” is a logical value that determines the form of the function. When cumulative is TRUE, NORMDIST returns the cumulative distribution function.

8) Perform the calculation for the 100 years flood again, this time using a period of only 20 years from anywhere in the record (make sure you state which period you chose).

9) Compare this result to the one obtained using the entire data set. How big a data set should you use? Why? What processes may prevent using the present data set for predictions of future flood magnitude and frequency?

Precipitation Prediction

Student exercise: Precipitation prediction

10) Upload the precipitation data for several cities in the US.

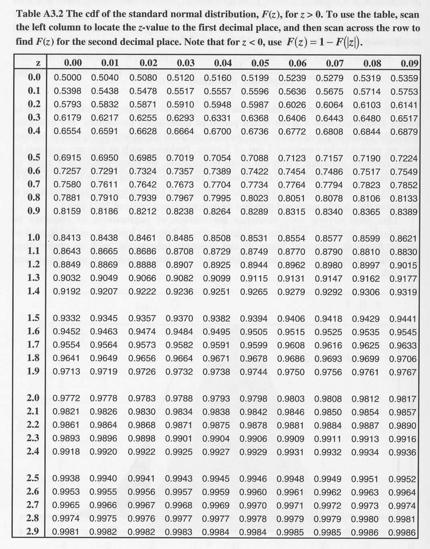
11) Use these data to calculate the 100 years rain event in the city of your choosing (ask yourself: which data you should use?). To perform this calculation, you should use the table below that provides cdf for any particular z-value.

12) Compare this value with the number of times measured precipitation did equal or exceed the prediction made in the previous question. Are they similar/different? Why?

13) Perform the calculation for the 100 years precipitation, this time using a period of only 20 years from anywhere in the record of the chosen city. Are the results similar? Explain why.

Challenge Question:

Identify a station in the U.S. for which you can obtain a time series for precipitation and for streamflow (visit the USGS web site: http://water.usgs.gov/waterwatch/). Is there a correlation between precipitation and streamflow? Why?