Relative maximum
Relative minimum
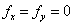
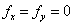
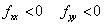
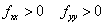
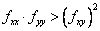
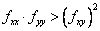
Slope and marginal values have basically the same interpretation in multivariate problems as they do in uinivariate problems. One of the benefits of multivariate processes is that economists can get a much richer interpretation of how variables act and interact.
Before we review the technical aspects of multivariate optimization, let's look at some examples of how we can use information about marginal values and rates of change.
Suppose that you are trying to understand the process of consumption and how economic agents evaluate and trade off utility as they decide what goods to purchase and consume. Without even knowing an exact utility function, we can make some predictions regarding this process by using the concepts of partial derivatives.
The partial derivative of utility with respect to consumption of good x can be interpreted as the marginal utility of x, or the amount of utility gained when a little more x is consumed. Suppose we are given the information that the ratio of the marginal utility of x to the marginal utility of y is one to one. How can we interpret this? Economists define this ratio as the marginal rate of substitution, and ues it to interpret how consumers evaluate tradeoffs in consumption of goods.
In virtually every area of economic behavior, slopes and rates of change from calculus operations can give information about how agents make decisions, such as how they value the next unit of consumption or the next unit of production, or the tradeoff between using labor vs. using capital, or the utility associated with one more unit of income.
Before we can interpret the information, however, we have to adapt our univariate techniques to multivariate functions.
The conditions for relative maxima and minima for multivariate functions are very similar to those for univariate functions, with one additional requirement.
First, all first-order partial derivatives must equal zero when evaluated at the same point, called a critical point. If we are considering a function z with two independent variables x and y, then the three-dimensional shape taken by the function z reaches a high or low point when evaluated at specific values of x and y; these values are determined by setting the first derivatives equal to zero, and then solving the resulting system of equations for the two variables.
Second, the second-order direct partial derivatives must both be the same sign when evaluated at the critical point(s). For a maximum, they must both be negative and for a minimum, both positive. This condition serves the same purpose as the second-order derivative condition in univariate optimization. It guarantees that the point where the slope is zero is indeed a high point, in the direction of the x variable and also in the direction of the y variable. This condition must be satisfied for both variables simultaneously, in order to rule out shapes of functions such as "saddle points."
To understand a saddle point, imagine a three dimensional shape, at a point where in one direction you are at the top of a hill (where the slope is zero), like being on a saddle where the shape is traced from the left to the right of the saddle. Now, turn 90 degrees. You are still at a point where the slope is zero, but the shape running from the back to the front of the saddle is now a valley and you are at the minimum.
For this type of a shape, the first order derivatives of x and y are zero, but the second order derivatives have different signs, meaning a relative maximum in one direction and a relative minimum in the other.
The third condition is rather technical. When evaluated at the critical point(s), the product of the second order partials must exceed the product of the cross partials. This condition rules out critical points that are neither points of maximum or minimum, but are points of inflection. A point of inflection is a point on a shape where certain conditions of optima are met, but the function does not actually take on the shape of a maximum or minimum.
To sum up, the points of optimum must have all of the following characteristics:
| Relative maximum |
Relative minimum |
|
|
|
|
|
|
|
|
|
Let's try an example. Given the following function, start by setting first derivatives equal to zero:
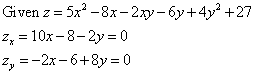
Using the technique of solving simultaneous equations, find the values of x and y that constitute the critical points.

Now, take the second order direct partial derivatives, and evaluate them at the critical points.
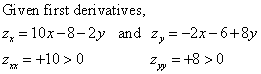
Both second order derivatives are positive, so we can tentatively consider the function evaluated at the critical point (x=1, y=1) to be a relative minimum. Now we take cross partials and check the final condition:
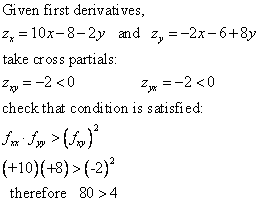
Note that it wasn't necessary to take both cross partials. Recall that in a previous section we noted that continuous functions will have identical cross partials. Therefore, either cross partial could have been used in the last condition, but taking both is a good way to check your work.
Constrained optimization is the technique of optimizing a function while adding an additional limit or constraint to the process. Typically, this constraint will be a budget (a monetary constraint) or process limitation (a physical constraint). Up to this point, all optimization problems have implicitly assumed that we could spend any amount of money on resources, and also use physically any amount of resources in order to optimize. This in one of the most unrealistic assumptions it is possible to make, and so the last technique we will review is a technique that allows constraints to be added to optimization processes.
The Lagrangian multiplier method incorporates a constraint into the body of the function being optimized in such a way that only if the constraint is met will the function reach its optimal point.
Let's illustrate this with an example.
Suppose our goal is to optimize Z, subject to the requirement that x and y equal 60:

Now, we can take derivatives of L, with respect to x, y, and our new variable λ. The result of forming this new function is that we have added the condition that in order for the derivative of L with respect to the variable λ to be equal to zero (a condition of optimization), the coefficient on the new variable must be equal to zero. Given the way the constraint is rearranged, the coefficient is zero only when the constraint is met. Therefore, the process of optimization now includes meeting the constraint as a condition of optimization.
Once the Lagrangian is formed, optimization is a very straightforward process. Take first derivatives, set equal to zero, and use the three equations to solve for the two choice variables:

The last step is to test whether the critical point is a maximum or minimum, using standard second order conditions where second derivatives greater than zero implies a minimum, less than zero a maximum.
[Index]