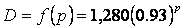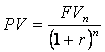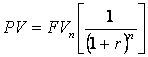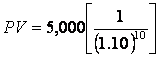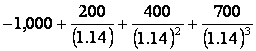The Exponential Function

The exponential function has the form:

            F(x) =  y  =  abx

 

where a ¹ 0 and  b is a constant called the base of the exponential function.  b > 0  and  b ¹ 1

 

x is the independent variable.  It is the exponent of the constant, b. Thus exponential functions have a constant base raised to a variable exponent

 

In economics exponential functions are important when looking at growth or decay.  Examples are the value of an investment that increases by a constant percentage each period ,  sales of a company that increase at a constant percentage each period, models of economic growth or models of the spread of an epidemic.

 

                                  


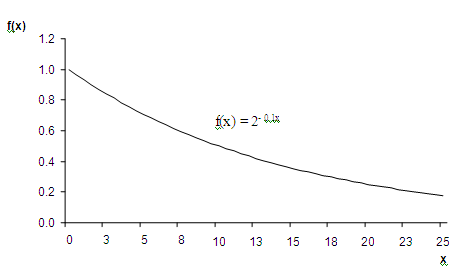
Notice that as the value of x increases, the value of y increases or decreases more and more rapidly.


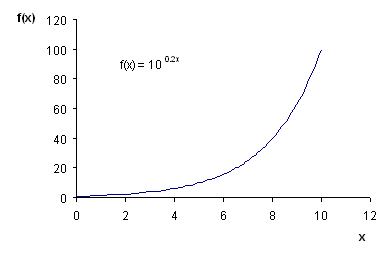
Examples of the exponential function

 

 

 

 

Applications of exponential functions

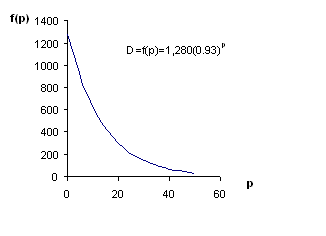
An exponential demand function

 

Demand for a product in thousands of units can be expressed by the following exponential demand function where p is the price in dollars:

 

           

 


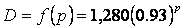
Compound interest - The time value of money

 

Financial decision making, whether by the private sector, the government or by households requires the evaluation of whether an expenditure is justified by the benefits it is expected to confer. The investment decision involves acquiring  something in the expectation that it will be worth more in the future. In financial terms this means purchasing an asset or assets which will provide future income. Typically the expenditure and the benefits occur at different points in time. Therefore sums of money occurring at different dates must be compared.

 

Examples of investment income include

The investment decision is the acquisition of a productive asset.

 

                            expenditure                                                     receipt(s)

 

                               outflow                                                            inflow(s)

The cash outflow is the expenditure of money in the present because of the expectation of the receipt of money in the future.

The cash inflow is the receipt of money in a future period or periods.

If the expected future inflow is greater than the present outflow then there is the expectation of a positive return which favors making the investment decision. Therefore the analysis of investment requires comparison of outflows with expected inflows.

Problem   The expenditure and the expected receipts occur at different periods In time.  Values of different periods are different values.  A value received in the future is not equivalent to a value received in the present.  Values occurring at different points in time cannot be immediately compared nor aggregated.

Solution  It is necessary to get a standardized unit of measurement.  The values of all the different periods must be transformed into units of standardized value.  They must be brought to the same point in time and then they can be compared and aggregated.

Thus to analyze an investment the cash outflows and the expected future receipts must be transformed into units of standardized value and then compared.  Then if the inflows are  greater than the outflows the investment has a positive rate of return and should be accepted.

 

Why does this problem exist?  An amount received in the future is not equivalent to an amount held in the present because money,  if invested at some rate of interest,  grows to a larger amount.  The interest rate is the rate at which an individual or an entity is compensated for exchanging money held in the present for money to be received at a future date.  Thus money has a time value and this value is called interest.

 

The standardization process:  transforming values of different periods into values of the same period

Compounding  Compounding means converting values of the present into values of the future.  It involves movement forward in time.  Compounding finds future values.  Compounding is used to find values at the ending point of an analysis.

Discounting  Discounting means converting values of future periods  to values of the present period.  It involves movement backward in time.  Discounting finds present values. Discounting is used to find values at the beginning point of an analysis.

Although the two procedures always yield the same decision, the discounting process is more commonly used for financial decision making. 

 

Notation

 

            PV        Present value

                         a value at time = 0

 

            FV        Future value

                         a value in some future period

                         the beginning amount plus accumulated compound interest

                         because the future has an infinite number of periods, these
                         periods are distinguished from each other by the use of subscripts.

 

                        FV1  = the value at the end of the first period

 

                        FV2  = the value at the end of the second period

 

                        FVn  = the value at the end of the nth period

 

It is important to note that in the future value notation, the future values are understood to occur at the end rather than at the beginning of the relevant future period.  The standard financial tables, financial calculators, and the spreadsheet Excel are all constructed with this understanding.

           

            r           the interest rate per period

                        the discount rate

 

            n          the number of periods in the analysis

 

Note     In finance discounting is the procedure for calculating present values.  However in retailing discounting is the procedure of reducing selling price in order to increase sales.


 

Future Values and compounding (single payments)

 

Compounding is the process of converting values of the present to values of the future.

 

We begin with present value.

What do we have at the end of the first period, i.e. what is FV1?

At the end of the first period we have our initial value, PV, plus the interest earned on that initial value, rPV.

 

            FV1    =  PV  +  rPV

 

            FV1    =  PV (1+r)

 

What do we have at the end of the second  period, i.e. what is FV2?

 

We begin the second period with FV1.

At the end of the second period we have what we began with, FV1, plus the interest earned on FV1.

 

            FV2   = FV1  +  r FV1

 

            FV2   = FV1 (1+r)

 

            FV2   = PV (1+r) (1+r)

 

            FV2   = PV (1+r)2

 

If we continued to calculate future values for all future periods we would note the subscript for the relevant future period is the same numerical value as the exponent for the expression (1+r).

 

It is thus possible to find a general expression for any future value

 

            FVn   = PV (1+r)n                        This is an exponential function of the form

 

            y       =  a bn                           where PV = a  and (1 + r) = b

 

In this expression the future value is determined by the value of r, the interest rate, and n, the time period.  Financial tables have been constructed for many possible values of r and n.  The expression, (1+r)n,  is known as the future value interest factor for a single payment, FVIFr,n where r is the interest rate and n is the number of periods.


 

Examples

 

1.  Deposit 100 and leave it  for twenty periods in an account which earns 4 percent per period.  How much will be in the account at the end of twenty periods?

 

            FV20  =  ?

 

            FV20  =  100 (1.04)20

 

            FV20  =  100 (2.1911)

 

            FV20  =  219.11

 

2.  Invest  2,000  in stock whose expected annual rate of return is 8 percent.  How much will you have  at the end of ten years?

 

            FV10  =  ?

 

            FV10  =  2,000 (1.08)10

 

            FV10  =  2,000 (2.1589)

 

            FV10  =  4,317.80

 

Present Values and discounting (single payments)

 

            Discounting  is the process of converting  expected future values to present  values.

 

            We begin with a future  value.

 

            FVn   = PV (1+r)n

 

           

 

           

 

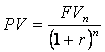
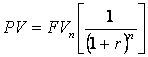
            PV = FV (PVIF n,r)

 

In this expression the present  value is determined by the value of r, the interest rate, and n, the time period.  Financial tables have been constructed for many possible values of r and n.  The expression, in square brackets,  is known as the present  value interest factor for a single payment, PVIF r,n where r is the interest rate and n is the number of periods.  Note that the present value interest factor for a  single payment  is the inverse of the future value interest factor.


 

Examples

 

1.  A financial instrument is expected  pay 5,000 in ten years.  The interest rate available today is 10 percent.  What would be a fair price for the claim to receive that 5,000 in ten years?

 

            PV  =  ?

 

           

 

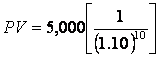
                PV  =  5,000 (.3855)      

 

            PV  =  1927.50

 

 

2.  An investment today is expected to generate a series of cash flows in the future such as the following:

 

            0                         -1,000                        investment expenditure

            1                             200                       

            2                             400                        receipts from the investment

            3                             700

 

An unsophisticated analyst might consider this a good investment because the sum of the receipts, 1,300, is greater than the investment expenditure, 1,000.  Such an analyst might consider that the investment offers a gain of 300.

 

However this is the wrong approach.  Values of different periods can  never be aggregated before they are standardized.  Failure to do so ignores the fact that funds available in the present can be invested to grow to some future value.  The correct approach to analyzing this investment is to discount each of the individual future values, then to aggregate them, and finally to compare the result to the initial investment expenditure.  If the available interest rate is 14 percent then

 

 

           

 

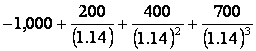
            -1,000  + 200 (.8772)  +  400 (.7695)  +  700 (.6750)  =  -44.26

 

Accepting this investment would actually create an immediate loss of 44 rather than a gain of 300.  This is an example of one of the basic methods of investment analysis, the net present value method or NPV.  It is called net present value because it adds the receipts net of the expenditure.

 

Note that the present value of a future value decreases as the discount rate increases and decreases the further into the future the cash flow occurs.

 

[Index]