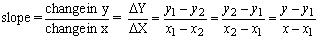
To write the equation of a line it is necessary to know the slope and the y intercept. There are three possibilities which depend on the data available.
Possibility 1
In this case both the slope and the y intercept are known and the equation can
be written directly.
For example if the slope is -2 and the y intercept is (0,6), then the equation is
y = 6 - 2x
Possibility 2
In this case the slope and one set of coordinates are known. This case involves
the use of the point-slope formula.
The point-slope formula
Here in the final term x1 and y1 are known coordinates
and x and y are unknown coordinates. Therefore the slope can be given as:
This expression is the point-slope formula. It can be rearranged to produce a working version.
y - y1 = b (x - x1)
y = y1 + b (x - x1)
Example
Find the equation of the line which has a slope of 4 and a set of coordinates (3,-2). Here x1 = 3 and y1 = -2.
y = y1 + b (x - x1)
y = -2 + 4(x-3)
y = -2 + 4x -12
y = -14 + 4x
Possibility 3
In this case two sets of coordinates are known but the slope is not known. This
case involves the use of the two-point formula. Since the slope of a linear
function is the same at any point on the line we may set an expression for the
value of the slope at one point equal to the value of the slope at any other
point.
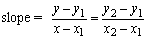 |
This expression is the two-point formula. |
Example
Find the equation of the line which passes through the points (-2,3) and (3,8).
x1 = -2 y1 = 3 x2 = 3 y2 = 8
[Index]