The linear function is popular in economics. It is attractive because it is simple and easy to handle mathematically. It has many important applications.
Linear functions are those whose graph is a straight line.
A linear function has the following form
y = f(x) = a + bx
A linear function has one independent variable and one dependent variable. The independent variable is x and the dependent variable is y.
a is the constant term or the y intercept. It is the value of the dependent variable when x = 0.
b is the coefficient of the independent variable. It is also known as the slope and gives the rate of change of the dependent variable.
Graphing a linear function
To graph a linear function:
1. Find 2 points which satisfy the equation
2. Plot them
3. Connect the points with a straight line
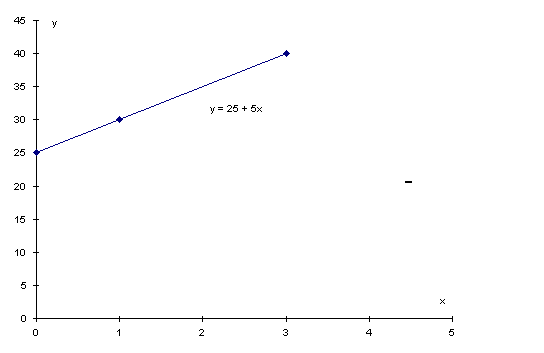
Example:
y = 25 + 5x
let x = 1
then
y = 25 + 5(1) = 30let x = 3
then
y = 25 + 5(3) = 40

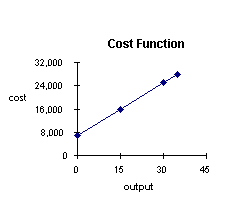
A simple example of a linear equation
A company has fixed costs of $7,000 for plant and equuipment and variable
costs of $600 for each unit of output.
What is total cost at varying levels of output?
let x = units of output
let C = total cost
C = fixed cost plus variable cost = 7,000 + 600 x
| output | total cost |
| 15 units | C = 7,000 + 15(600) = 16,000 |
| 30 units | C = 7,000 + 30(600) = 25,000 |
Combinations of linear equations
Linear equations can be added together, multiplied or divided.
A simple example of addition of linear equations
C(x) is a cost function
C(x) = fixed cost + variable cost
R(x) is a revenue function
R(x) = selling price (number of items sold)
profit equals revenue less cost
P(x) is a profit function
P(x) = R(x) - C(x)
x = the number of items produced and sold
Data:
A company receives $45 for each unit of output sold. It has a variable cost
of $25 per item and a fixed cost of $1600.
What is its profit if it sells (a) 75 items, (b)150 items, and (c) 200 items?
R(x) = 45x C(x) = 1600 + 25x P(x) = 45x -(1600 + 25x) = 20x - 1600
| let x = 75 | P(75) = 20(75) - 1600 = -100 a loss |
| let x = 150 | P(150) = 20(150) - 1600 = 1400 |
| let x = 200 | P(200) = 20(200) - 1600 = 2400 |
[Index]