The quadratic function has the form:
F(x) = y = a + bx + cx2
where a, b, and c are numerical constants and c is not equal to zero.
Note that if c were zero, the function would be linear.
An advantage of this notation is that it can easily be generalized by adding more terms. We could for example write equations such as
y = a + bx + cx2 + dx3
y = a + bx + cx2 + dx3 + ex4
In many books quadratic equations are written as
ax2 + bx + c = 0
In this case the quadratic formula is given by
Note that the denominator is then 2a instead of 2c.
Some common examples of the quadratic function
Notice that the graph of the quadratic function is a parabola. This means it is a curve with a single bump. The graph is symmetric about a line called the axis of symmetry. The point where the axis of symmetry intersects the parabola is known as the vertex.
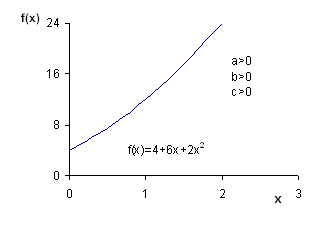
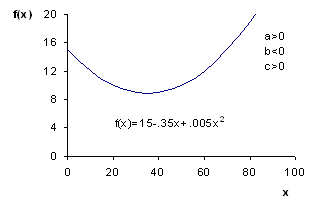
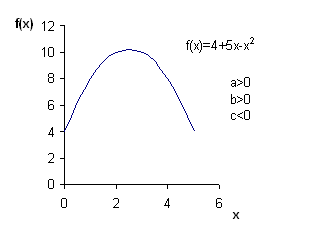
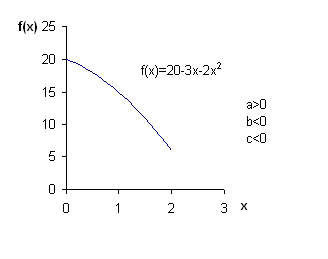
Construct a table with values of x and f(x).
Plot the data points.
Connect the data points with a smooth line.
This is easily done with Excel.
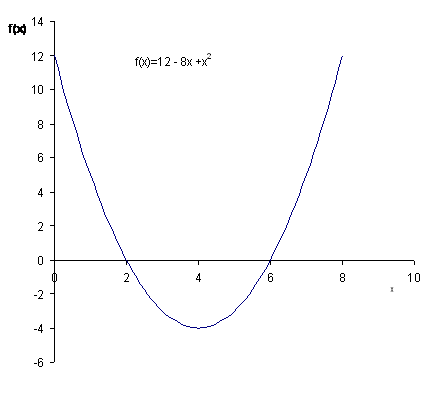
Example 1 f(x) = 12 - 8x +x2
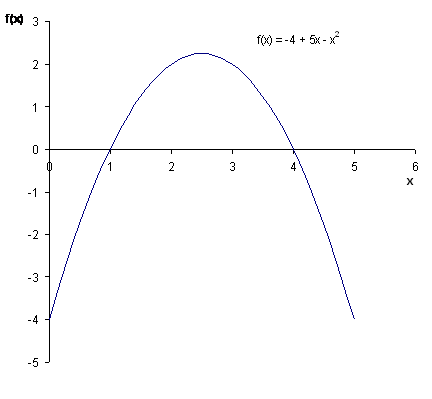
Example 2 f(x) = -4 + 5x -x2
The quadratic formula, an example.
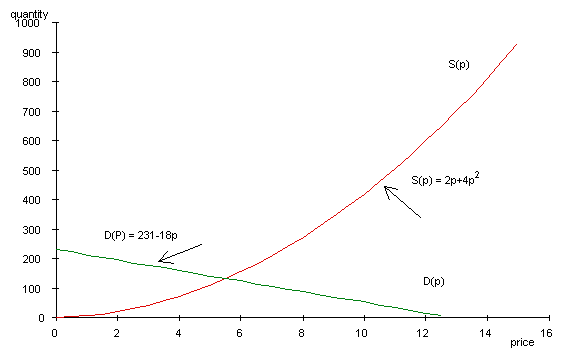
In general the supply of a commodity increases with price and the demand decreases. The market for the commodity is in equilibrium when supply equals demand.
In this example we are considering two functions of the same independent variable, price. We want to find the equilibrium price and the corresponding demand.
The supply function is a quadratic equation given by S(p) = 2p + 4p2
The demand function is a linear function given by D(p) = 231 - 18p
To find the intersection of the two curves set supply equal to demand and solve for p.
S(p) = 2p + 4p2 = 231 - 18p = D(p)
After collecting terms we obtain the quadratic equation
231 - 20p -4p2 = 0
Note that this has the form of the quadratic equation
y = a + bx + cx2
0 = 231 -20p -4p2
Solve the equation by means of the quadratic formula where a = 231, b = -20, and c = -4.
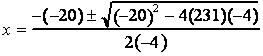
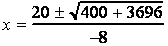
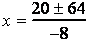
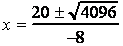
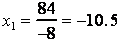 and
and 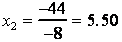
Since price cannot be negative the value of -10.5 can be eliminated. Supply will equal demand when the price is $5.50. At that price it is possible to find the corresponding demand and supply.
D(5.50) = 231 - 18(5.50) = 132
S(5.50) = 2(5.50) + 4(5.502 = 132
[Index]