Finding the slope of a linear function is straightforward. Furthermore the slope is the same at each point on the function. However this is not the case with non-linear functions. A non-linear function does not have a constant slope.
Consider the non-linear function shown below. What is the slope at some point such as P? (P can be at any point along the curve.) It can be seen that the slope of the function depends on the position of P on the curve.
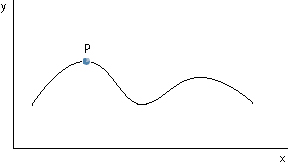
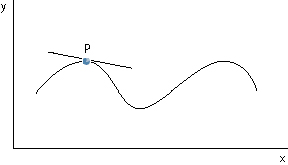
The problem is to find the slope of the function at point P. A possible solution is to draw a line tangent to the non-linear function at point P as shown in the following chart. The tangent line touches the function but does not intersect it. The slope of this tangent line is the same as the slope of the non-linear function at point P.
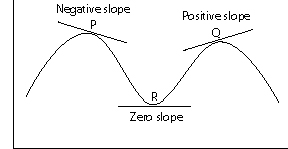
The slope of a non-linear function is different at different points along the function. The slope may be positive, negative or zero as indicated by the tangent lines in the following chart. The value obtained for the slope depends on the point on the function where the tangent line is drawn.
[Index]