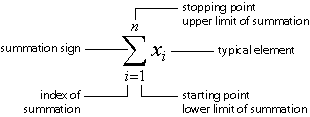
Often mathematical formulae require the addition of many variables Summation or sigma notation is a convenient and simple form of shorthand used to give a concise expression for a sum of the values of a variable.
Let x1, x2, x3, …xn denote a set of n numbers. x1 is the first number in the set. xi represents the ith number in the set.
Summation notation involves:
The summation sign
This appears as the symbol, S, which is the Greek
upper case letter, S. The summation sign, S, instructs us to sum the elements of
a sequence. A typical element of the sequence which is being summed appears
to the right of the summation sign.
The variable of summation, i.e. the variable which is being summed
The variable of summation is represented by an index which is placed beneath
the summation sign. The index is often represented by i. (Other common possibilities
for representation of the index are j and t.) The index appears as the expression
i = 1. The index assumes values starting with the value on the right hand side
of the equation and ending with the value above the summation sign.
The starting point for the summation or the lower limit of the summation
The stopping point for the summation or the upper limit of summation
Some typical examples of summation
|
This expression means sum the values of x, starting at x1 and ending with xn. |
|
This expression means sum the values of x, starting at x1 and ending with x10. |
|
This expression means sum the values of x, starting at x3 and ending with x10. |
|
The limits of summation are often understood to mean i = 1 through n. Then the notation below and above the summation sign is omitted. Therefore this expression means sum the values of x, starting at x1 and ending with xn. |
|
This expression means sum the squared values of x, starting at x1 and ending with xn. |
Arithmetic operations may be performed on variables within the summation. For example:
|
This expression means sum the values of x, starting at x1 and ending with xn and then square the sum. |
Arithmetic operations may be performed on expressions containing more than one variable. For example:
|
This expression means form the product of x multiplied by y, starting at x1 and y1 and ending with xn and yn and then sum the products. |
|
In this expression c is a constant, i.e. an element which does not involve the variable of summation and the sum involves n elements. |
Data
|
i |
xi |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
1. Find |
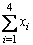 |
2. Find |
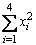 |
Data
|
i |
xi |
|
1 |
-1 |
|
2 |
3 |
|
3 |
7 |
and c which is a constant = 11
3. Find |
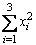 |
4. Find |
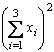 |
5. Find |
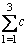 |
Data
|
i |
xi |
yi |
|
1 |
10 |
0 |
|
2 |
8 |
3 |
| 3 | 6 | 6 |
| 4 | 4 | 9 |
|
5 |
2 |
12 |
6. Find |
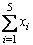 |
7. Find |
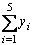 |
8. Find |
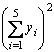 |
9. Find |
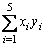 |
[Index]