Copyright © Wayne A. Wickelgren. All rights are reserved, except permission is granted for noncommercial copying of any part of the article in any form provided the above reference and this copyright notice are part of the copy.
Wickelgren, W.A. (1997) Idea roles, idea families, and the syntax of purposive cognition in the cerebral cortex. In W.A. Wickelgren, Ed. Cognition & Neuroscience 1997, pp. 1-17. New York: Wicweb Press. http://www.columbia.edu/~ww50/
An idealized model of a computing unit of the mammalian cerebral cortex is described in terms of families of nodes representing related idea roles. Each idea family has 13 roles: occur, expect, deny (negate), want, nont (wanting the negation), relevant, irrelevant, gain, loss, plan, scheme, get, and avoid. Consider the idea family for "your eating an apple." The occur node of this family is active when this sensory event occurs. The expect node is active when you consciously think of this event. The deny node is active when you expected the event, but it did not occur. The want (nont) node is active when you want (do not want) the event to occur. The gain and loss nodes represent the expected positive and negative utility of the event. The get node is active when you execute an action program to try to make the event happen. The plan node is active when you plan such an action program before executing it. The avoid node is active when you execute an action program to avoid the occurrence of the event. The scheme node is active when you plan an avoidance program. Each family encapsulates perception, attention, cognition, motivation, and action within a functional unit of knowledge representation. The internal connection structure of an idea family is innate and largely unmodifiable. The connections between nodes in different families are innate, but learning modifies their strength to represent both the constituent structure of knowledge and the sequential structure of knowledge. The model is applied to the analysis of planning, decision making, and execution of action programs.
In his book, Animal Intelligence, Thorndike (1911) attributed the evolutionary superiority of the human mind over lower animal minds to a greater analysis by humans of vague wholistic ideas into their component parts. Thorndike stressed abstractive S-R learning, in which the common attributes of some class of stimuli, to which a response is rewarded, get most strongly linked to that response, while the more variable attributes are less strongly linked. Since humans, could abstract more precise attributes of situations, they were better able to associate a response with the correct set of stimulus attributes.
Although one theme in the evolution of intelligence is indeed the evolution of new stimulus analyzing mechanisms, this is not the primary superiority of the human mind over lower animal minds. Thorndike was almost entirely wrong in this respect.
Thorndike was also wrong in characterizing human learning as being via the S-R reinforcement mechanism. Almost all of conscious human learning is cognitive, as is much of the learning of all mammals and birds, while most or all of the associative learning of lower vertebrates, fish and amphibia, is either classical conditioning or instrumental conditioning via Thorndike's S-R reinforcement mechanism (Tolman, 1948, Bitterman, 1969, 1975).
A comparison of food seeking in humans vs. fish exemplifies the distinction between cognitive and S-R learning. When you open your refrigerator door, you have expectations of specific foods to be found there. When a fish swims into a familiar patch of reeds, however, it may have no idea what it will find, though seeing that patch elicited a very strong urge to swim into it, due to many prior occasions in which the fish found food there.
The role of reinforcers such as food and water differs in two ways between S-R and cognitive learning. On the one hand, a motivationally significant reinforcer is essential for S-R learning to occur, whereas cognitive learning occurs in free exploration, with no reinforcers beyond the novelty of the environment and no drive besides curiosity. On the other hand, the reinforcer is not a part of what is learned in S-R learning, whereas the consequences of actions are very much a part of what is learned when a mammal learns cognitive expectancies.
Elsewhere, I have discussed evidence that it is the cerebral cortex of mammals that learns cognitive expectancies, while subcortical learning is S-R (Wickelgren, 1979).
I also argue that the cerebral cortex exhibits a new type of learning mechanism, namely, chunking, that recruits neurons to represent novel combinations of already represented ideas (Wickelgren, 1979, 1987). This vertical associative capacity goes beyond the previously available horizontal associative capacity characteristic of classical conditioning and S-R learning. Specifically, I believe that the chunking learning mechanism is essential to cognitive learning, but not for S-R learning.
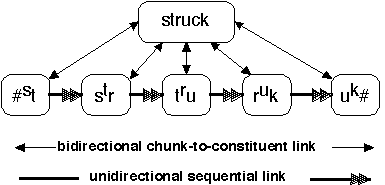
Figure 1 illustrates how neurons representing phonetic segments might be chunked by having strong links to one or more neurons representing the word composed of these segments. You will note that the segments are not phonemes, but overlapping triples of phonemes, which I call context-sensitive allophones (Wickelgren, 1969a, 1969b).
There are many reasons to prefer context-sensitive allophones over phonemes as the immediate constituents of words. The most important reason is that overlapping triple coding represents sufficient information concerning the order of the phonemes to permit articulation in the correct order and also auditory discrimination of words that are permutations of the same phonemes, such as "struck, trucks, and crust."
The bidirectional vertical links represent the chunk-to-constituent links that are strengthened by the chunking process. The unidirectional horizontal links are strengthened by ordinary associative learning via contiguous activation, e.g., activation of the str will often be followed by activation of the tru.
Figure 1. Words as Chunks of Context-Sensitive Allophones

In addition to the chunking learning mechanism, a second distinguishing feature of cognitive minds is the development of cognitive modules of neurons, in addition to the sensory and motor modules present in lower organisms. Cognitive modules contain neurons representing objects, actions, events, concepts, and propositions pertaining to the world, not just patterns or sequences of features within a single sensory or motor modality.
Neurons representing cognitive ideas such as the idea of an object must be activatable by many different types of sensory and cognitive events. When we activate an idea in such a cognitive system we do not automatically activate all of our knowledge of that idea, but the associations to that idea are all available for activation in relevant contexts.
A cognitive system is a knowledge system, rather than a system for representing what is activating our senses at the moment, though such perceptual knowledge is often part of what is active at any given time in a cognitive system. Cognitive systems are a step removed from perception and action. They are repositories of knowledge of the world over all time, not just the part of the world currently experienced by our senses.
From a process standpoint, in addition to storing knowledge of the world, the cognitive system has inferential and planning capacity. It can use stored knowledge in combinations to derive much more knowledge than ever was directly stored, and it can use knowledge to make plans for achieving goals. Whether inferring and planning are different mechanisms or different viewpoints on the same mechanism is an interesting unsolved problem. In this paper I concentrate on planning, decision, and execution of action programs to achieve concrete goals. I ignore inference and abstract thinking.
In a recent book on learning and emotion, Livesey (1986) argues that emotion is a characteristic of more advanced minds, not primitive minds. Livesey believes that emotion and cognition evolved together. This coevolution began with fish or whatever Metazoans can be instrumentally conditioned, since instrumental conditioning requires representation of the affective consequences of actions in order for animals to learn either correct S-R associations or correct expectations of consequences.
Consistent with Livesey, an idea I develop here is that the cerebral cortex has a cognitive representation of motivation and emotion in the form of wants and nonts. Nont is a made-up word that means to want for something not to occur. Nont is the opposite of want. Much to my surprise, want seemed to have no opposite word in English; so I made up one. The basic idea is that we can want or nont anything that we can think of.
In this paper, I describe a simple idealized model of a knowledge module in the cerebral cortex. The model represents declarative and procedural knowledge, motivation, emotion, utility, expectation, perception, attention, planning, decision, and execution of action programs to obtain goals. The development of this model is far from complete.
The model is an abstract semantic net whose nodes represent ideas, not individual neurons. A node might require several or many neurons each to implement in the brain. This is a psychological model, not a neural model, and no assumption is being made as to whether the nodes that represent ideas use specific neuron ("grandmother cell") coding, multiple nonoverlapping neural set coding, distributed overlapping neural set coding, or neural activation pattern coding. To minimize confusion, I try to use the terms "node" and "link" in discussing this model of the mind and the terms "neuron" and "synapse" in speculating about the brain.
As has been frequently noted, the cerebral cortex seems to employ the same kinds of neurons with the same types of connections throughout. The anatomical structure of the cerebral cortex appears to feature a repetition of some type of cortical computing unit. This paper presents an idealized psychological model for such a cortical computing unit, which I call an idea family.
The basic assumption is that ideas come in families, with a fixed set of roles in each family. Note that an idea may be as elementary as a specific sensory attribute, such as a red line in a certain location in the visual field, or as complex as an embedded metacognitive proposition, such as "I know that Norma told Peter that she would be home late today."
The present model has 13 nodes in each idea family representing the roles: occur, expect, deny, want, plan, get, nont, scheme, avoid, gain, loss, relevant, and irrelevant. To provide a fast introduction to the meaning of these roles, we can do no better than to consider an example idea family, namely, "your eating an apple."
If you are eating an apple, the occur node for this family is active, whether or not you are consciously thinking about eating the apple. If you expect to eat an apple under some conditions, the expect node is active. If you are consciously aware of eating an apple at the present moment, both the occur and the expect node for this are active. When you finish eating an apple or when you expected to eat an apple and did not, the deny node becomes active.
When you want to eat an apple, the want node is active. If you want to eat an apple and the expectation of being able to do so is not too low, the plan node for eating an apple is activated. Activating the plan node causes a recomputation of the likelihood of your being able to eat an apple if you attempt, in the present context, to execute the action program for eating an apple. The expect node changes its degree of activation to reflect the subjective probability that you will succeed in eating an apple if you execute the action program to do so.
The gain node represents something similar to the subjective expected utility of attempting to eat an apple in the present context. If the (expected) gain is sufficiently large in comparison to the (expected) loss from executing the apple-eating action program, you will make the decision to activate the get node in the apple eating family. The active get node is now the top node of an action program that uses information concerning your present location, the remembered location of apples, etc. to try to achieve the goal of eating an apple. Should you succeed in eating an apple, the occur node in this apple-eating family will be activated, and this will terminate activity in this family, unless you decide you want a second apple.
When you find the idea of eating an apple unpleasant, the nont (not want) node is active. When you nont to eat an apple, but you expect you may have to, the scheme node becomes active, if the activation of the (expected) loss node is high enough relative to other expected gains and losses. Activation of the scheme node causes a change in the activity of the expect node, conditional upon the likely effectiveness of your actions to avoid eating an apple. If the new expected loss is reduced enough, a decision is made to activate the avoid node, initiating an action program to avoid eating an apple.
An easy way to remember the terminology of appetitive planning vs. aversive scheming is to think "plan to get" and "scheme to avoid."
When either the want or nont node for eating an apple is strongly activated, the relevant node is active. When eating an apple has neither much positive or negative utility, then repeated occurrences or strong expectations of apple eating will activate the irrelevant node, which will inhibit conscious thought about this, as in habituation.
The present model describes one type of idea family that might be used in a module of the mind that represents our knowledge of the physical world, including our knowledge of goals and of the consequences of our actions. In addition to this knowledge module, there are doubtless many other modules at both a cortical and a subcortical level. For example, some or all of the occur nodes in the knowledge module must receive sensory input from lower-level cortical sensory modules, and some or all of the action nodes, get and avoid, must output to lower-level cortical motor modules.
Precise understanding of the role of each node in a network mind comes from understanding its links to other nodes in the network and ultimately to the world outside the mind. Since complete models of animal minds will probably have millions, billions, or even trillions of nodes, we must analyze these nodes into equivalence classes of nodes that have identical patterns of connection to nodes in their own class and other classes.
A successful model of idea families will have one or a small number of different types of idea families in a single module, with each type having equivalent internal and external link structure throughout the module. In particular, this means that there must be the same number of nodes in each idea family of the same type.
Equivalent internal, within-family, link structure means that if the occur node has an excitatory link to the expect node in one family in the knowledge module, the occur node in any other family has the same type of excitatory link to the expect node in that other family, and similarly for every other pair of roles within a family.
Equivalent external, between-family, link structure means that if the occur node of family i projects to the get node of a different family j, then this is true for all families i _ j in the knowledge module.
Equivalent internal, within-family, link structure means that the directed graph of nodes and links within a family is isomophic to that of every other family of the same type within the module. It obviously does not mean equal levels of activation of corresponding nodes (that is, the same roles) in different idea families of the same type at the same time.
Equivalent external, between-family, link structure means that the same roles of different idea families have equivalent links to nodes outside their own family. If the external link structure of idea families is deterministic such that either role i connects to role j in all other idea families or in none of them, then equivalent external link structure means that the set of external roles to which role i in idea family k is connected is identical for all idea families. Although the number of synapses per neuron in the cerebral cortex is insufficient for every neuron to synapse directly with every other neuron, distributed coding of ideas by a large enough set of neurons will permit full connectivity of idea nodes at a functional (psychological) level.
In this model, the innate connection structure of the mind is represented by a directed graph with a number of different types of nodes and links, a doubly chromatic digraph, where we think of types of nodes and types of links as being represented visually by different colors. Certain parameters of nodes and links such as the threshold of nodes and the rate of decay of potential of links or the time delay parameter of links may be innate and participate in the typing (coloring) of nodes and links.
Other parameters such as the strength (weight) of a link are affected by associative learning and change slowly with experience. Still other parameters such as the activation of a node and the potential of a link represent the current thoughts of the mind and its short-term memory, and change rapidly with experience.
Corresponding nodes of different idea families represent different ideas, so all modifiable node and link parameters that are affected by experience must generally be nonequivalent. It is the innate link structure of idea families that is equivalent, not the learned structure.
I limit discussion of external link structure to links between pairs of nodes in different idea families inside the knowledge module. These between-family links are shown in Figure 2. Not included are links to nodes in other modules.
Figure 2. Between Family Link
Structure
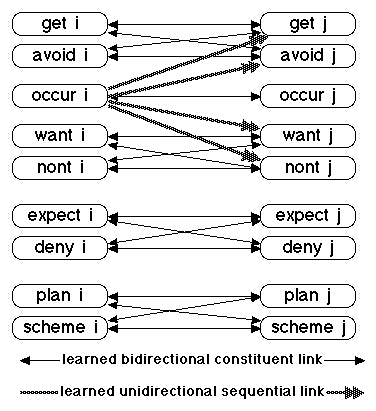
A knowledge module might contain an arbitrarily large number of nodes, and human knowledge modules probably require millions or billions of nodes. A model that describes all of these between-family links with the simple diagram of Figure 2 is an enormous simplification. For example, if there are a million families in the knowledge module, Figure 2 represents all of the entries in a 13 million by 13 million square connection matrix that contains almost 169 trillion entries, actually 169 trillion minus the 169 million entries in the within-family connection matrix.
Note that there are two types of links between idea families: the bidirectional links represent the constituent structure of knowledge and the unidirectional links represent the sequential structure of knowledge. An example of both constituent and sequential structure was shown in Figure 1. The vertical links between the word "struck" and its unordered set of constituent allophones is an example of constituent structure. The horizontal links that specify the order of the allophones is an example of sequential structure.
Both types of links are excitatory, and both are modifiable by associative learning. However, learning constituent structure requires both associative learning capacity and chunking capacity. Learning sequential structure requires only associative learning by correlated activation as suggested by Hebb (1949).
Four of the 13 roles, gain, loss, relevant, and irrelevant, do not appear in this diagram because they have no links to nodes in other families of the knowledge module. That does not mean that they have no external links. Gain and loss have output links to decision making nodes in a metacognitive module, as will be discussed later, and relevant and irrelevant may receive some input links from motivational nodes and/or arousal nodes in other modules.
The bidirectional constituent links of the nine roles are organized into the singleton occur node and four pairs: get and avoid, want and nont, expect and deny, plan and scheme. Each member of each pair has both input and output links to each member of the pair in every other family. That is, all of these links are bidirectional. They satisfy the reverse link hypothesis, namely, that if node i links to node j, then there is a reverse link from node j to node i.
The only input to occur nodes from nodes in the knowledge module is from other occur nodes. Occur nodes are organized in a heterarchical manner, with the lowest-level nodes receiving input from sensory modules. Thus, occur nodes are activated only by sensory input and constitute a rather pure representation of the sensory world at the moment.
Expect j receives input from the expect and deny nodes of other families that indicates the strength of evidence that i will occur in the world currently being simulated by the knowledge system, which may or may not be the current sensory environment. Deny j receives input from the expect and deny nodes of other families that indicates the strength of evidence against j's occurrence in the simulated world.
Want and nont nodes receive external input from other want and nont nodes in the knowledge module that represents the subgoal constituent structure of wants and nonts. They also receive input from subcortical motivational modules, that represent the degree of deprivation of various desirable entities for want nodes or the presence of noxious entities for nont nodes.
Get and avoid link to other get and avoid nodes in a manner that represents which actions are subgoals of what other actions. A set of active get and avoid nodes constitutes an action program. Currently, I think of an action program as having a single top-level get or avoid node, but this may not be necessary.
A completely parallel set of bidirectional constituent links connects goal plans and schemes to subgoal plans and schemes, so that one can plan an action program prior to deciding whether or not to execute it.
The sequential structure of knowledge is represented by the four unidirectional between-family links emanating from the occur role and going to the get, avoid, want, and nont roles of other families. Basically, this is an S-R type of knowledge, with sensory events tending to activate motivation and action. The smell of the popcorn makes you want to eat popcorn. The occurrence of the event of holding the popcorn in your fingers triggers the next component of the popcorn eating program, namely putting the popcorn into your mouth.
Want and nont nodes do not just represent
the needs of the body as signalled by internal deprivation detectors.
Want and nont nodes also receive input from occur nodes in the
present model. This influences mammalian motivation to be
opportunistic, pursuing goals that are more likely to be achievable
in the current environment. For organisms with a multiplicity of
goals, making motivation dependent upon goal availability as well as
degree of need may be sensible, though it is more straightforward to
let availability influence decisions concerning actions than to have
it contaminate the representation of needs and desires. A mechanism
to achieve the latter is incorporated in the model for within-family
link structure to be discussed next.
Figure 3. Within Family Link Structure
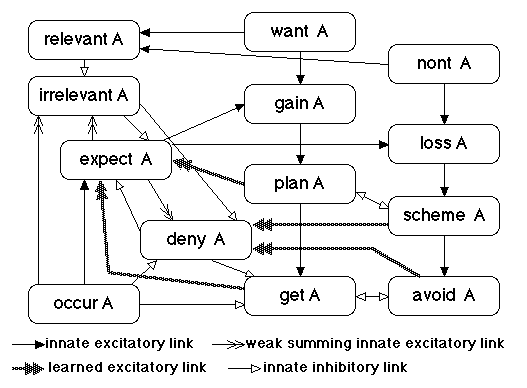
Figure 3 describes the internal link structure of idea family A. Though far less than the number of between-family links, the number of within-family links described by this single diagram is 169 million, in a hypothetical knowledge module with a million idea families.
There are four different types of within-family links. Three of these are innate, that is, unmodifiable by learning in their strength and decay properties, though link potentials vary over time in a way that constitutes a kind of short-term memory. The short, solid black arrowheads represent strong innate excitatory links with a fast decay of link potential. The thin, double-headed arrowheads represent weak innate excitatory links with a slow decay of link potential. The white arrowheads represent strong innate inhibitory links. The large fuzzy grey arrowheads represent the only learnable links within an idea family.
This paper will not discuss the relevant and irrelevant nodes, relevant A and irrelevant A, that control attentional set, and this paper will only discuss the function of some of the links among the remaining nodes.
Three nodes have no input links from other nodes within the family: occur, want, and nont.
If the world being simulated is the current sensory environment, then some metacognitive module enables the links from occur to expect nodes within a family, so that we consciously think about stimuli impinging on us. Such thinking about the current environment is perception in the model. We can then compute expectations of future input in the current environment based on past knowledge stored by the strengths of between-family links among expect and deny nodes.
Deny A inhibits expect A. Thus, expect A represents the net superiority, if any, of the evidence for A occurring minus the evidence against A occurring. The activation of expect A represents something like the subjective probability of A occurring in the simulated world.
The two modifiable excitatory input links from plan and get A to expect A and the two comparable links from scheme A and avoid A to deny A represent how effective the action nodes, get A and avoid A have been in the past in increasing or decreasing the probability of A's occurrence, averaged over all contexts. A distributed memory version of this model will likely represent this information via modifiable between-family links and permit the elegant assumption that all within-family links are innate.
Gain A receives excitatory links from want A and expect A, such that the activation of gain A is the product of the activation of want A and expect A. Gain A represents something like idea family A's expected positive utility of the current action program. Loss A provides the same estimate of the negative utility component contributed by A.
Gain A and loss A send excitatory links to plan A and scheme A. respectively, that will activate one or the other of these nodes, provided there are not competing gain and loss nodes that activate their plan and scheme nodes more actively.
Get and avoid have mutually inhibitory links, because whatever ambivalence we may have in our wanting and nonting of A, it is a logical absurdity to try to get and avoid A simultaneously. A mammal may alternate between approach and avoid behavior, but it cannot do both at once. For the same reason, a mammal should either plan to approach A or to avoid A at a particular point in an action program, but not both.
I define choice to be deciding which of several alternative action programs is best. I define decision to be deciding whether or not to execute a single program.
In an S-R model of mind, one rule handles both choice and decision That rule is to execute the action which is most strongly activated by the present internal and external stimulus context, provided the level of activation of this action is above some threshold, else do nothing. Since learning has conditioned the nodes that represent stimulus elements to those actions that previously brought positive reinforcement, survival is enhanced, though only additive contingencies can be learned.
Choice among two or more alternative actions and the go no-go decision whether or not to execute an action are not distinguished in the S-R model. All decision making is based on a combination of doing nothing, if no alternative action exceeds a threshold, and choosing the most strongly activated alternative among those that exceed the threshold. This single decision rule is possible because S-R minds do not plan. S-R minds either execute an action program or they do nothing.
Choice and decision are not so easy to model in a cognitive mind. You may recall Guthrie's (1952) criticism of Tolman's cognitive model that Tolman left the rat in the maze, lost in thought, unable to move. It was a valid criticism.
Cognitive minds mentally generate novel action programs, infer likely consequences of these programs, evaluate how good a program is likely to be, compare the expected utility of that program to the expected utility of the best prior program, and decide whether or not the goodness of the best program is good enough to execute as opposed to doing nothing or continuing to plan. In cognitive minds, choice and decision probably should be distinguished, though both may be based on the expected utilities of alternative action programs.
Due to lack of time, I will say no more about multiple choice comparison of action programs and restrict my attention to how the expected utility of a single action program is determined and how the decision is made as to whether or not to execute that program, as outlined in Figure 4.
Figure 4. Decision to Execute a
Program
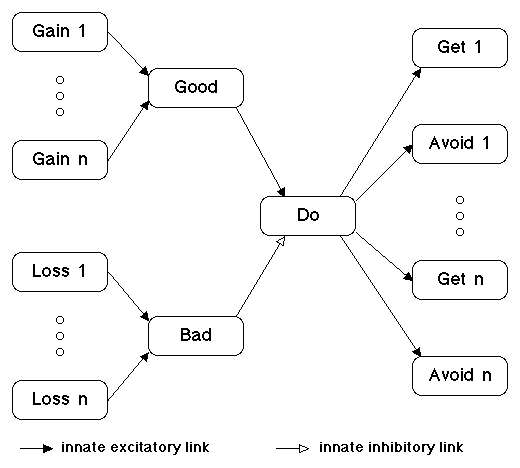
Each of the millions of idea families in the knowledge module has gain and loss nodes that measure the expected positive and negative utility from the viewpoint of that idea family. This assessment of expected utility occurs at all times in all idea families. If no action program is being planned, that is, no plan and scheme nodes are activated, then the gain and loss nodes of each family represent the expected utility of doing nothing. If some action program is being planned, then the gain and loss nodes measure the expected utility of the simulated world that includes execution of that action program. The utility of an action program is the difference in total expected utility from executing the action vs. doing nothing.
To sum the utility contributions of each idea family, it is simple and plausible to assume overall good and bad nodes to which all specific gain and loss nodes are innately linked, as illustrated in Figure 4.
Note that gain i and loss i will contribute to the total judged utility of a planned action program, regardless of whether that program includes plan i, scheme i or neither one. Although this says that decisions are based on unidimensional utilities, the composite utilities for any choice may differ from time to time with the state of the mind as reflected in the level of activation of different drives, as well as with learned modification of the association of various nodes with different types of reward, punishment, pleasure, and pain. Hopefully, treating utility as a composite of components whose weightings are subject to such motivational and learned modification will avoid certain problems with the utility concept, while preserving its virtue as a simple, plausible vehicle on which to base decision making.
The good node measures the total positive utility of the present action program. The bad node represents the total negative utility. The do node receives excitatory input from the good node and inhibitory input from the bad node.
The do node does not perform a simple simultaneous comparison, deciding to execute a plan if good exceed bad by some threshold amount. Rather, the do node performs a sequential comparison of the good minus bad difference for the current program vs. the prior program. The do node adapts to whatever difference of good vs. bad input it is receiving, and is activated when the net positive utility of the current program exceeds that of the prior program by some threshold amount. This is what is required both to decide to execute an appetitive program to achieve a positive goal because that program increases utility above the zero of doing nothing and to decide to execute an aversive program to avoid a negative goal because that program decreases the negative utility of doing nothing.
The do node implements the decision by sending output to all get and avoid nodes, activating any get or avoid node which is currently receiving sufficient input from its plan or scheme node, and initiating execution of the action program represented by the currently active get and scheme nodes.
I limit my discussion of planning to appetitive goal behavior, and I rely primarily on an example. Consider again the idea family where A represents the event "you eating an apple." Suppose you want to eat an apple, so that want-A is active, but you are in a context where the activation of the expect node for eating an apple is fairly low. First off, it might be that the expectation, while low, is far enough above zero that a strong want could result in sufficient expected net gain to cause you to decide to try to get-A, that is, to get to eat an apple, without any further planning of the details of how you are going to achieve this goal. You might then have to do some planning during execution.
Alternatively, you might defer your decision to get to eat an apple until you had done more planning. In planning, goal wants propagate activity to subgoal wants and nonts in other idea families. In the present example, subgoals might include asking someone nearby concerning the availability of apples in the vicinity, remembering locations where apples are found, such as in refrigerators, stores, on apple trees, etc., to see if any of these subgoal wants matches with an expect. For example, you may remember that there is a market nearby that probably sells apples. This addition to the action program jacks up the expected gain and may trigger the decision to execute the eat-an-apple program.
The essence of planning is that goal wants activate subgoal wants, while the expect nodes are activating each other to achieve a model of the context being simulated. When there is a convergence of wants and expectations with sufficiently great expected net positive utility, then the plan nodes in that family are activated.
Action programs are fleshed out by having plan and scheme nodes activate their constituents to consider the program in more detail. The complete set of plan and/or scheme nodes that constitutes the currently considered action program results in an altered level of activation of expect A, via the internal, within-family, feedback loop and via an external, between-family, feedback loop through changes in contextual expectations.
If the total expected increase in net utility is great enough, then the decision is made to execute the currently planned program.
Figure 5. Subgoal Structure: Nail
Hammering
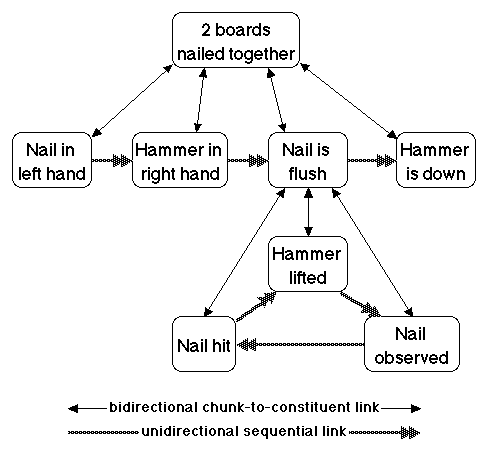
Let us consider the execution of a three-level action program whose top goal is to activate the occur node of idea family T. The immediate constituents of T are the ordered set of ideas A, B, C, and D. If you wish, you may interpret this as a small part of an action program to attach two boards by hammering a nail through one and into the other until it is flush with the surface of the top board, as in Miller, Galanter, and Pribram (1960). T means nail the board together. A means hold the nail in your left hand over the target. B means get the hammer in your right hand. C means hammer the nail flush. D means lay down the hammer. The nail hammering interpretation is diagrammed in Figure 5.
I believe that our minds code such ordered sets by means of unordered sets of context-sensitive constituents, such that each constituent can be represented by a triple of symbols where the middle symbol represents a class of "equivalent" ideas, the initial symbol represents an equivalence class of predecessor ideas in thought, and the terminal symbol represents an equivalence class of successor ideas. In context-sensitive coding, T is actually #T#. The constituents of T are: #AB, ABC, BCD, CD#. Note that # means the juncture or break between programs. The context-sensitive coding of the program is shown in Figure 6.
Figure 6. Context-Sensitive Coding of
Action Program
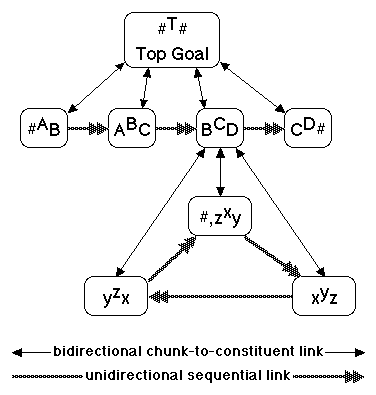
The constituents of C are a subroutine that must be executed repeatedly in a loop until occur C is activated when the nail is flush. The constituents of C are: x=nail hit, y=hammer lifted, z=nail observed. Of course, this is just a small part of any real nail hammering program. Many aspects of the problem are ignored. T has more constituents; the other constituents of T have constituents, as do the constituents of x, y, and z. But this small piece of a program is sufficient for my purposes.
Each of the ideas T, A, B, C, D, x, y, z is an idea family with all 13 roles, but only some of these roles are involved in executing the action program.
Execution begins when the do node sends activation to all get and avoid nodes. A get or avoid node that is the top node of some action program, a node of the type #-# , requires input from two sources to become fully activated: the do node and a plan or scheme node. Non-top, initial get and avoid nodes, nodes of type #-- , also require a third input via vertical downward constituent links from their chunk nodes. All other l inks also require a fourth input via horizontal sequential links from the prior occur node.
Thus, get T is activated by a combination of input from plan T and do, since get T is a top node. Get T remains active until the entire T program has been successfully executed, and occur T becomes activated.
As soon as get T is active, it provides the necessary third input to activate its initial constituent, get #AB. Activation of occur #AB provides the necessary sequential condition for activating the next constituent, get ABC.
So far, we have not discussed the looping illustrated in the x, y, z subroutine. The initial constituent of the loop is family #,zxy , which is the x that is either initial or preceded by z and (in either case) is followed by y. As an initial constituent, get #,zxy , is activated by do, plan #,zxy , and its superordinate chunk, get C. Get x leads to activation of occur x. This activates get y, and activation continues to flow around the x, y, z loop in this way until occur C is activated. When occur C is activated, this inhibits get C and eliminates the necessary downward vertical input that kept the x, y, z loop alive. When a superordinate get is inhibited, all of its constituent gets cease being activated.
Activation of occur C also actives get D, which is followed by occur D, then occur T, and the entire T program has been successfully executed.
We can return to the more concrete version of this action program by referring again to Figure 5. The branching and looping consists of hitting the nail, lifting the hammer, observing whether or not the nail is flush, repeating the loop if the nail still sticks up, and terminating the hammering if it is flush.
Like many, I am intrigued with the distinction between declarative and procedural knowledge. Despite considerable thinking about it, I am very dissatisfied with my understanding of the distinction.
Idea families can be used to define a distinction between declarative knowledge as represented by the between-family constituent links among occur, expect, and deny roles and procedural knowledge as represented by the between-family constituent links among plan, scheme, get, and avoid roles.
Bearing in mind that these two types of constituent knowledge may not be too representative of what is called declarative and procedural knowledge in other contexts, it is nevertheless interesting to note that the goal-subgoal knowledge, which was the focus of this paper, appears to have a declarative constituent structure that is isomorphic to its procedural constituent structure.
For example, each constituent of the action program for hammering a nail in Figure 5 is described not in terms of the action performed, but in terms of the goal achieved. Psychologists have known for some time that the response learned by mammals in instrumental learning is an equivalence class of actions that accomplish some goal. This insight is represented in the model by having both perceptual and action roles in every idea family in the knowledge module and having the constituents of get T be a set of get and avoid nodes whose activation increases the probability of T occuring.
I am not convinced that all human cognitive knowledge ought to be represented by idea families with exactly the same roles described in this paper. For example, I do not now see the value in having a get node for a classificatory proposition such as "penguins are birds," but maybe I will someday. More likely, the types of roles in an idea family will vary somewhat for different cortical modules.
However, for goal-subgoal knowledge, it may be that when perception strengthens the links between the occur and expect nodes of constituent idea families, A, B, C, and D and the occur and expect nodes of chunk idea family T, the links between the want, plan, and get nodes of T and the want, plan, and get nodes of A, B, C, and D are also strengthened. When planning and execution of an action program succeed in activating the occur roles for the desired goals, this ought to strengthens links between the motivational, planning, and action roles of a chunk and its constituents and also strengthen connections between chunks and their constituents for the perceptual and cognitive roles of the chunk family. Declarative and procedural knowledge are not identical in this model, but they might be isomorphic in constituent structure.
For example, when a child first watches an adult hammer a nail, the child may learn many or all of the components of the nail hammering program simply by observation. The child's perception of the adult holding the hammer in one hand, holding the nail in the other, and pounding until the nail is flush may establish both the constituent structure and the sequential structure of the nail hammering program in the knowledge module.
Of course, if the child's observation is incomplete, the constituents of the program may be incomplete. The nail hammering program is surely incomplete vis a vis contextual changes, such as when the hammer and nails must be located or purchased, when the nail bends, when the nail must be driven in at other than a 90 degree angle, etc. Finally, lower-level motor modules intervene between the knowledge module and actual motor output. If the child's strength or coordination are inadequate, execution of the hammering program may not accomplish the goal.
Despite all of these complications, it is clear that humans often learn knowledge-level representations of procedures from observation and imitation of others, not just from Thorndikean trial and error.
Some of what it means to have a cognitive mind at the human level, as opposed to an S-R mind is to know what to expect from events and actions, to learn from observation and imitation perhaps motivated by curiosity alone, to evaluate everything, to plan many alternative action programs, and to choose which program to execute based on expected value of its consequences compared to those of the alternative action programs considered.
The idea role-family model is designed to capture these and many other aspects of what it means to have a cognitive mind. Although the model may seem strange at first, it appears to have considerable potential to express general principles that characterize human cognition.
Bitterman, M. E. (1969). Thorndike and the problem of animal intelligence. American Psychologist, 24, 444-453.
Bitterman, M. E. (1975). The comparative analysis of learning. Science, 188, 699-709.
Hebb, D. O. (1949). The organization of behavior. New York: Wiley.
Guthrie, E. R. (1952). The psychology of learning. Revised. New York: Harper & Row.
Livesey, P. J. (1986). Learning and emotion: a biological synthesis. Vol. 1: Evolutionary Processes. Hillsdale, NJ: Erlbaum.
Miller, G. A., Galanter, E., & Pribram, K. H. (1960). Plans and the structure of behavior. New York: Holt-Dryden.
Thorndike, E. L. (1911). Animal intelligence. Reprinted by New York: Hafner, 1965.
Tolman, E. C. (1948). Cognitive maps in rats and men. Psychological Review, 55, 189-208.
Wickelgren, W. A. (1969a). Context-sensitive coding, associative memory, and serial order, in (speech) behavior. Psychological Review, 76, 1-15.
Wickelgren, W. A. (1969b). Context-sensitive coding in speech recognition, articulation, and development. In K. N. Leibovic (Ed.), Information processing in the nervous system (pp. 85-96). New York: Springer-Verlag.
Wickelgren, W. A. (1979). Chunking and consolidation: a theoretical synthesis of semantic networks, configuring in conditioning, S-R versus cognitive learning, normal forgetting, the amnesic syndrome, and the hippocampal arousal system. Psychological Review, 86, 44-60.
Wickelgren, W. A. (1987). Site fragility theory of chunking and consolidation in a distributed memory. In N. W. Milgram, C. M. MacLeod, & T. L. Petit (Eds.), Neuroplasticity, learning and memory. (pp. 301-325). New York: Alan R. Liss.