Economics W3213

Professor Xavier PRESENTS...

Problem Set 3: The Lion King

(1) The Circle of Life

(a) Botswana has aggregate wage bill of 60 billion dollars and an aggregate GDP of 100 billion. The aggregate GDP growth rate over the last 10 years was 10 percent (that is ) and the growth rates of capital and labor were 10 percent () and 5 percent () respectively. What was the PRODUCTIVITY growth rate for this country? Before you start, make sure you compute the "capital share ()" and the "labor share ()".

(b) Consider the economy in the previous question. Imagine that aggregate GDP is the SAME, but the wage bill is 80 billion instead of 60. What is the growth rate of productivity now? If it is different, explain why intuitively.

(c) Repeat parts (a) and (b) under the assumption that . If your answers are different, explain why intuitively.

(2) I Can't Wait to be King

Consider the Solow-Swan growth model, with a savings rate, s, a depreciation rate, , and a population growth rate, n. The production function is given by

where A and B are positive constants. Note that this production is a mixture of Romer's AK model and the neoclassical Cobb-Douglas production function.

(i) Does this production function exhibit constant returns to scale? Explain why.

(ii) Does it exhibit diminishing returns to capital? Explain why.

(iii) Express output per person, y=Y/L, as a function of capital per person, k=K/L.

(iv) Write down an expression for y/k as a function of k and graph. (Hint: as k goes to infinity, does the ratio y/k approach zero?)

(v) Use the production function in per capita terms to write the fundamental equation of the Solow-Swan model.

(vi) Suppose first that . Draw the savings curve and the depreciation curve. What number does the savings curve approach as k goes to zero? As k goes to infinity, the savings curve approaches a number: what number is that? Is it zero?

(vii) Under these parameters, will there be positive growth in the long run? (Remember that A and B are constants). Why?

(viii) Imagine that we have two countries with the same parameters (same A, B, s, , and n). One of them is rich and the other is poor. Which one of the two will grow faster? Why? Does this model predict convergence?

(ix) Suppose now that . Draw the savings and depreciation curves. Under these circumstances, will there be positive growth in the long run? Why?

(x) If s=0.4, A=1, B=2, and n=0.02, the growth rate converges to some value as time goes to infinity. What is this value?

(3) Hakuna Matata

Discuss the following economic concepts:

    (A) Public Good

    (B) Non-Rival Good

    (C) Non-Excludable good.

In your discussion, you may provide examples of each type of goods.

Is technology a Rival or non-Rival good? Is it always non-excludable? Discuss the role of excludability as it relates to the incentives may have to develop new ideas. 

(4) Be Prepared 

(A) President Mbeki of South Africa decided to allow pharmaceutical firms in his country to produce the three antiretroviral generics that help patients with HIV slow down the development of full blown AIDS. Do you think this is a good idea? Please give the pros and cons of this policy.

(B) Professor Michael Kremer of Harvard proposed the creation of an AIDS fund that would purchase vaccines that prevent AIDS to help African countries. Do you think this is a good idea?   Please give the pros and cons of this policy.

(5) Can you feel the love tonight?

Imagine that a country faces two production functions. The first production function is a regular Cobb Douglas:

The second technology requites a fixed set up cost per person F (think of an infrastructure cost) which must be paid every at every instant:

Once the fixed cost is paid, the second technology is more productive so that B>A.

 

(a)    Derive output PER WORKER for each of the two production functions and DRAW output per worker as a function of capital per worker. Imagine that the economy must use either one production function or the other (but not both at the same time). For what level of k will technology A be used? For what level of k will technology B be used?

(b)   What is the EFFECTIVE production function? (That is, for every level of capital, draw the production function that will be actually be used). Is this effective production function concave? EXPLAIN INTUITIVELY WHY YOU GET THESE RESULTS.

(c)    Derive the fundamental equation of the Solow-Swan model.

(d)   Draw the savings curve for an economy facing the effective production derived in class

(e)    Draw the depreciation line and describe how the economy behaves for all levels of capital.

(f)     How does the economy converge to the steady state for all values of ψ and B? Explain your results.

(g)    Suppose that the World Bank donates a little bit of capital to this economy. How will k behave over time? What if the donation is very large? Explain.

(h)    Jeffrey Sachs has used this model to justify a large increase in international development aid to poor countries. Do you think this is a good argument?

(6) Warthog Rapsody

Consider a Solow-Swan economy with a Cobb Douglas production function

Imagine that the savings rate, “s”, is an increasing function of capital and it has the following functional form: for low values of k the savings rate is constant at some low level. For intermediate levels of k, the savings rate increases rapidly. For high levels of k the savings rate is constant again. In other words, the savings rate looks like:

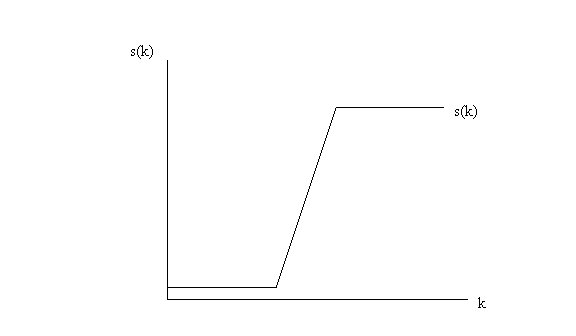
(a)    As usual, the “savings line” is equal to savings rate times the average product of capital so it is given by . Draw the savings line if s(k) is the savings rate described in the figure above.. Draw the depreciation line.

(b)   How many steady states do you have? Discuss the stability properties of the steady state (or steady states if you found many).

(c)    Does this model predict poverty traps?