Research in the Reichman Group

(A) Optical and Electronic Properties of Layered Materials

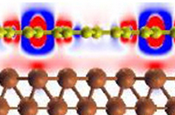
Effort in the Reichman group has recently been aimed at understanding the behavior of novel two dimensional materials such as graphene, transition metal dichalcogenides and their heterostructures. Using electronic structure techniques we have successfully described the electronic properties of chemically doped graphene,1,2,3,4 bilayers of molybdenum disulfide,5 as well as the structural and electronic behavior of grain boundaries in transition metal dichalcogenides.6 Recently we have developed a simple theory that combines electronic structure theory with simple analytic elements for the excitonic properties of transition metal dichalcogenides. This theory has been shown to provide a quantitative description of excition, trion, and biexciton binding energies,7 as well as the excited state optical properties of these novel materials.8

Click an image:

Layered 1 Layered 2 Layered 3
(B) Energy Transport in the Condensed Phase and in Photovoltaic Materials

The Reichman group is carrying out theoretical research to devise novel approaches for the description of exciton transport in complex condensed phase systems. The goals of this work are both fundamental and practical, with the applied component of the work directed towards optimizing the conversion of solar radiation to electrical energy. We have developed reduced density matrix theories that successfully describe general microscopic aspects of energy transport in condensed media,9,10 biological systems,11 and the process of singlet fission in organic crystals, whereby singlet excitons may rapidly and efficiently transform to multiple lower energy triplet excitons.12,13,14,15,16 This process may provide a means of increasing the efficiency of solar cells.

Click an image:

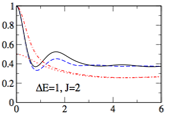
Energy 1 Energy 2 Energy 3
(C) Out-of-Equilibrium Dynamics and Transport in Quantum Systems

Our group studies a wide variety of problems that involve the quantum behavior of correlated electronic systems that are driven out of equilibrium via contact to reservoirs held at different chemical potentials or temperatures or via a sudden change of interaction parameters (a "quantum quench").17 Our group uses analytical tools (e.g. bosonization) and has developed new numerical tools (e.g. iterative path-integral based schemes and exact real-time quantum Monte Carlo techniques) to investigate these problems.18,19,20,21,22,23

Click an image:

Trans 1 Trans 2 Trans 3
(D) Statistical Mechanics of Disordered and Glassy Systems

Understanding the transition from a liquid to a glass has been called "the deepest and most interesting unsolved problem in solid state theory." Our group investigates the behavior of supercooled liquids and glasses using both analytical and computational tools. The Reichman group has made major contributions to understanding the role of activated transport and the onset of glassy dynamics in supercooled liquids,24,25 the description of non-linear susceptibilities related to dynamical heterogeneity26,27,28 and the connection between structure and dynamics in supercooled liquids.29 Currently a major effort in the group is aimed at distinguishing purely kinetic scenarios of the glass transition from those driven by non-trivial changes in the entropy of available configurations.30

Click an image:

Glass 1 Glass 2 Glass 3
(E) Structure, Dynamics, Rheology and Self-Assembly of Soft Materials

For several years a major thrust of research in the Reichman group has been the theoretical description of the behavior and assembly of "soft" materials (colloidal suspensions, gels, membranes, polymer networks, etc). Our efforts in this broad area have spanned a range from analytical work (e.g. our work on sheared colloidal suspensions31,32), to coarse grained modeling (e.g. our work on non-equilibrium self-assembly of networks of nanoparticles33), to atomistic molecular dynamics and Monte Carlo simulations (e.g. our work on the interplay between microphase separation and gelation in charged attractive colloidal systems34 and more recent work on conjugated polymer modeling35,36,37). In this area we often collaborate with experimental groups at Columbia and elsewhere.

Click an image:

Soft 1 Soft 2 Soft 3
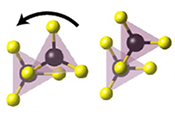
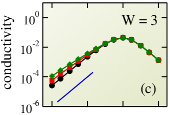
(F) Quantum Liquids and Glasses

We have developed a microscopic theory to understand the dynamics of quantum fluids such as liquid para-Hydrogen.38 Our theory is in good agreement with transport and scattering experiments in these systems. Motivated by recent experimental and computational work suggesting novel features that arise from an interplay between intrinsically quantum mechanical fluctuations and glass formation, we have used our approach to predict how quantum fluctuations modify classical scenarios of the glass transition.39,40 In a slightly different context we are investigating under what conditions interactions can lead to equilibration of an otherwise non-ergodic assembly of particles or spins. A prime example of this type of quantum glass phenomena is the putative "many-body" localization transition whereby a non-ergodic Anderson-localized system may equilibrate if particle interactions are strong enough. We are investigating this transition using a variety of analytical and numerical approaches.41,42

Click an image:

Quantum 1 Quantum 2 Quantum 3
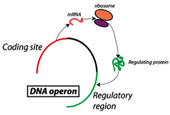
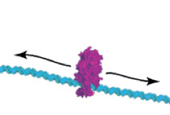
(G) Biophysical Transport

Our group has maintained an interest in biological transport problems such as how proteins find active sites along DNA43 and RNA44 and how biological cargo diffuse inside the crowded cellular environment.45 Some of this work has been motivated and carried out with various experimental groups at Columbia, such as the Greene Lab (Columbia Medical School) and the Prives Lab (Columbia Biology).

Click an image:

Bio 1 Bio 2 Bio 3

References
  1. L. Zhao, R. He, K. T. Rim, et al., Visualizing Individual Nitrogen Dopants in Monolayer Graphene. Science 333, 999-1003 (2011).
  2. T. Schiros, D. Nordlund, L. Pálová, et al., Connecting Dopant Bond Type with Electronic Structure in N-Doped Graphene. Nano Letters 12, 4025 (2012).
  3. L. Zhao, M. Levendorf, S. Goncher, et al., Local Atomic and Electronic Structure of Boron Chemical Doping in Monolayer Graphene. Nano Letters 13, 4659 (2013).
  4. A. Zabet-Khosousi, L. Zhao, L. Pálová, et al., Segregation of Sublattice Domains in Nitrogen-Doped Graphene. Journal of the American Chemical Society 136, 1391 (2014).
  5. A. M. van der Zande, J. Kunstmann, A. Chernikov, et al., Tailoring the Electronic Structure in Bilayer Molybdenum Disulfide via Interlayer Twist. Nano Letters 14, 3869 (2014).
  6. A. M. van der Zande, P. Y. Huang, D. A. Chenet, et al., Grains and grain boundaries in highly crystalline monolayer molybdenum disulfide. Nature Materials 12, 554 (2013).
  7. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Theory of neutral and charged excitons in monolayer transition metal dichalcogenides. Physical Review B 88, 045318 (2013).
  8. A. Chernikov, T. C. Berkelbach, H. M. Hill, et al., Non-Hydrogenic Exciton Rydberg Series in Monolayer WS2. Physical Review Letters 113, 076802 (2014).
  9. S. Jang, Y.-C. Cheng, D. R. Reichman and J. D. Eaves, Theory of coherent resonance energy transfer. Journal of Chemical Physics 129, 101104 (2008).
  10. T. C. Berkelbach, D. R. Reichman and T. E. Markland, Reduced density matrix hybrid approach: An efficient and accurate method for adiabatic and non-adiabatic quantum dynamics. Journal of Chemical Physics 136, 034113 (2012).
  11. T. C. Berkelbach, T. E. Markland and D. R. Reichman, Reduced density matrix hybrid approach: Application to electronic energy transfer. Journal of Chemical Physics 136, 084104 (2012).
  12. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Microscopic theory of singlet exciton fission. I. General formulation. Journal of Chemical Physics 138, 114102 (2013).
  13. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of superexchange. Journal of Chemical Physics 138, 114103 (2013).
  14. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Microscopic theory of singlet exciton fission. III. Crystalline pentacene. Journal of Chemical Physics 141, 074705 (2014).
  15. W.-L. Chan, T. C. Berkelbach, M. R. Provorse, et al., The Quantum Coherent Mechanism for Singlet Fission: Experiment and Theory. Accounts of Chemical Research 46, 1321 (2013).
  16. E. Busby, T. C. Berkelbach, B. Kumar, et al., Multiphonon Relaxation Slows Singlet Fission in Crystalline Hexacene. Journal of the American Chemical Society 136, 10654 (2014).
  17. M. S. Foster, T. C. Berkelbach, D. R. Reichman and E. A. Yuzbashyan, Quantum quench spectroscopy of a Luttinger liquid: Ultrarelativistic density wave dynamics due to fractionalization in an XXZ chain. Physical Review B 84, 085146 (2011).
  18. D. Segal, D.R. Reichman, and A.J. Millis, Nonequilibrium quantum dissipation in spin-fermion systems. Physical Review B 76, 195316 (2007).
  19. E. Gull, D. R. Reichman and A. J. Millis, Bold-line diagrammatic Monte Carlo method: General formulation and application to expansion around the noncrossing approximation. Physical Review B 82, 075109 (2010).
  20. E. Gull, D. R. Reichman and A. J. Millis, Numerically exact long-time behavior of nonequilibrium quantum impurity models. Physical Review B 84, 085134 (2011).
  21. G. Cohen, E. Gull, D. R. Reichman, et al.Numerically exact long-time magnetization dynamics at the nonequilibrium Kondo crossover of the Anderson impurity model. Phys. Rev. B 87, 195108 (2013).
  22. G. Cohen, D. R. Reichman, A. J. Millis and E. Gull, Green's functions from real-time bold-line Monte Carlo. Physical Review B 189, 115139 (2014).
  23. G. Cohen, E. Gull, D. R. Reichman and A. J. Millis, Green's Functions from Real-Time Bold-Line Monte Carlo: Spectral Properties of the Nonequilibrium Anderson Impurity Model. Physical Review Letters 112, 146802 (2014).
  24. R.A. Denny, D.R. Reichman, and J.P. Bouchaud, Trap models and slow dynamics in supercooled liquids. Physical Review Letters 90, 025503 (2003).
  25. Y. Brumer and D.R. Reichman, Mean-field theory, mode-coupling theory, and the onset temperature in supercooled liquids. Physical Review E 69, 041202 (2004).
  26. G. Biroli, J.P. Bouchaud, K. Miyazaki, et al., Inhomogeneous mode-coupling theory and growing dynamic length in supercooled liquids. Physical Review Letters 97, 195701 (2006).
  27. L. Berthier, G. Biroli, J.-P. Bouchaud, et al., Spontaneous and induced dynamic correlations in glass formers. II. Model calculations and comparison to numerical simulations. Journal of Chemical Physics 126, 184504 (2007).
  28. L. Berthier, G. Biroli, J.-P. Bouchaud, et al., Spontaneous and induced dynamic fluctuations in glass formers. I. General results and dependence on ensemble and dynamics. Journal of Chemical Physics 126, 184503 (2007).
  29. A. Widmer-Cooper, H. Perry, P. Harrowell, and D.R. Reichman, Irreversible reorganization in a supercooled liquid originates from localized soft modes. Nature Physics 4, 711-715 (2008).
  30. G. M. Hocky, T. E. Markland and D. R. Reichman, Growing Point-to-Set Length Scale Correlates with Growing Relaxation Times in Model Supercooled Liquids. Physical Review Letters 108, 225506 (2012).
  31. K. Miyazaki and D.R. Reichman, Molecular hydrodynamic theory of supercooled liquids and colloidal suspensions under shear. Physical Review E 66, 050501 (2002).
  32. K. Miyazaki, D.R. Reichman, and R. Yamamoto, Supercooled liquids under shear: Theory and simulation. Physical Review E 70, 011501 (2004).
  33. E. Rabani, D.R. Reichman, P.L. Geissler, and L.E. Brus, Drying-mediated self-assembly of nanoparticles. Nature 426, 271 (2003).
  34. P. Charbonneau and D.R. Reichman, Phase behavior and far-from-equilibrium gelation in charged attractive colloids. Physical Review E 75, 050401 (2007).
  35. G. Bounos, S. Ghosh, A. K. Lee, et al., Controlling Chain Conformation in Conjugated Polymers Using Defect Inclusion Strategies. Journal of the American Chemical Society 133, 10155-10160 (2011).
  36. K. H. DuBay, M. L. Hall, T. F. Hughes, et al., Accurate Force Field Development for Modeling Conjugated Polymers. Journal of Chemical Theory And Computation 8, 4556 (2012).
  37. M. C. Traub, K. H. DuBay, S. E. Ingle, et al., Chromophore-Controlled Self-Assembly of Highly Ordered Polymer Nanostructures. Journal of Physical Chemistry Letters 4, 2520 (2013).
  38. E. Rabani and D.R. Reichman, A fully self-consistent treatment of collective fluctuations in quantum liquids. Journal of Chemical Physics 120, 1458-1465 (2004).
  39. T. E. Markland, J. A. Morrone, B. J. Berne, et al., Quantum fluctuations can promote or inhibit glass formation. Nature Physics 7, 134-137 (2011).
  40. T. E. Markland, J. A. Morrone, K. Miyazaki, et al., Theory and simulations of quantum glass forming liquids. Journal of Chemical Physics 136, 074511 (2012).
  41. T. C. Berkelbach and D. R. Reichman, Conductivity of disordered quantum lattice models at infinite temperature: Many-body localization. Physical Review B 81, 224429 (2010).
  42. Y. Bar Lev and D. R. Reichman, Dynamics of many-body localization. Physical Review B 89, 220201(R) (2014).
  43. J. Gorman, A. Chowdhury, J.A. Surtees, et al., Dynamic basis for one-dimensional DNA scanning by the mismatch repair complex Msh2-Msh6. Molecular Cell 28, 359-370 (2007).
  44. F. Wang, S. Redding, I. J. Finkelstein, et al., The promoter-search mechanism of Escherichia coli RNA polymerase is dominated by three-dimensional diffusion. Nature Structural And Molecular Biology 20, 174 (2013).
  45. J.D. Eaves and D.R. Reichman, The subdiffusive targeting problem. Journal of Physical Chemistry B 112, 4283-4289 (2008).