A Center for Scientific
Research Using Calculating Machines
Miss Eleanor Krawitz
Tabulating Supervisor
Watson Scientific Computing Laboratory
Columbia Engineering Quarterly, November 1949
DURING recent years great strides have been made in all fields of scientific research, and a major factor in this advancement has been the extensive use of automatic computing methods and equipment. Today calculations are performed automatically in laboratories throughout the country. The development of these computing laboratories is of particular interest to Columbia students since the earliest ones were established here at the University. The Columbia University Statistical Bureau was established in the late twenties for the use of educators and statisticians. The Astronomical Bureau, created in 1934, directed by Dr. W. J. Eckert, and operated jointly by Columbia University, the American Astronomical Society, and International Business Machines Corporation, functioned as a non-profit organization where astronomers from all over the world could come to have their calculations performed. In 1945 IBM created a Department of Pure Science, appointed Dr. Eckert as its director, and founded the Watson Scientific Computing Laboratory on the University campus.
The primary purpose of the Watson Laboratory is research in the various branches of science, especially those involving applied mathematics and numerical calculation. The services of the laboratory are offered gratuitously to any scientist or graduate student engaged in research which makes a significant contribution to progress in the fields of science, and which uses calculating machines to achieve that end. Each year two Watson Laboratory fellowships in applied mathematics are awarded to students whose study or research involves large-scale computations. Members of the staff offer courses of instruction in their field of interest under the auspices of different departments of the University. Courses for graduate students include the operation and use of the machines, and numerical methods; academic credit for the courses may be obtained by registering with the University in the usual manner. Special classes in the operation of the machines are given at regular intervals to professional people, visiting scientists from all over the world, and graduate students working for their Doctorate degrees. An additional function of the Watson Laboratory is the dissemination of technical information concerning mathematical machine methods and mathematical tables; a comprehensive library covering these subjects is available.
Research has been successfully completed in many fields of science at the laboratory by members of the staff and visiting scientists. The following is a partial list of projects completed or in progress:
- Astronomy: integration of orbits of planets and asteroids,
- Geophysics: tracing of paths of sound waves under water for various depths and directions,
- Optics: calculations embodying the method of ray tracing,
- Chemistry: computation of quantum mechanical resonance energies of aromatic compounds,
- Engineering: building of Spring and Gear tables and computing stress calculations associated with earthquake loads,
- Economics: estimates of certain coefficients in the equations of economic models, using matrix multiplication and inversion,
- Physics: calculations of calcium transitional probabilities,
- Crystallography: evaluation of a Fourier Transform for the structure of insulin.
Most of the machines read and write through the use of the punched card which furnishes a means of handling data automatically. The cards can thus be processed through any series of calculators and have any desired sequence of operations performed on them. The primary advantage of the punched card technique is that a large number of similar operations can be performed in quantity. After punching initial values on the cards, the machine procedure is automatic. Punching may take place in any one of eighty columns of the card. Each column is subdivided into twelve distinct positions, representing the integers 0 to 9 as well as two special punching positions referred to as X and Y. The X punch is used principally to designate a special operation or a negative number. Letters of the alphabet are recorded by two punches in a column, a combination of an X, Y, or 0, with any one of the integers 1 to 9 (see fig. 1).

Figure 1. Tabulating Card showing 12 punching positions
and combinations of punches to indicates letters.
In all machines the principle of reading the card is the same. The holes are punched into the cards and are read by means of electrical contacts made through the holes. The card, acting as an insulator, passes between a wire brush and a brass roller (see fig. 2).
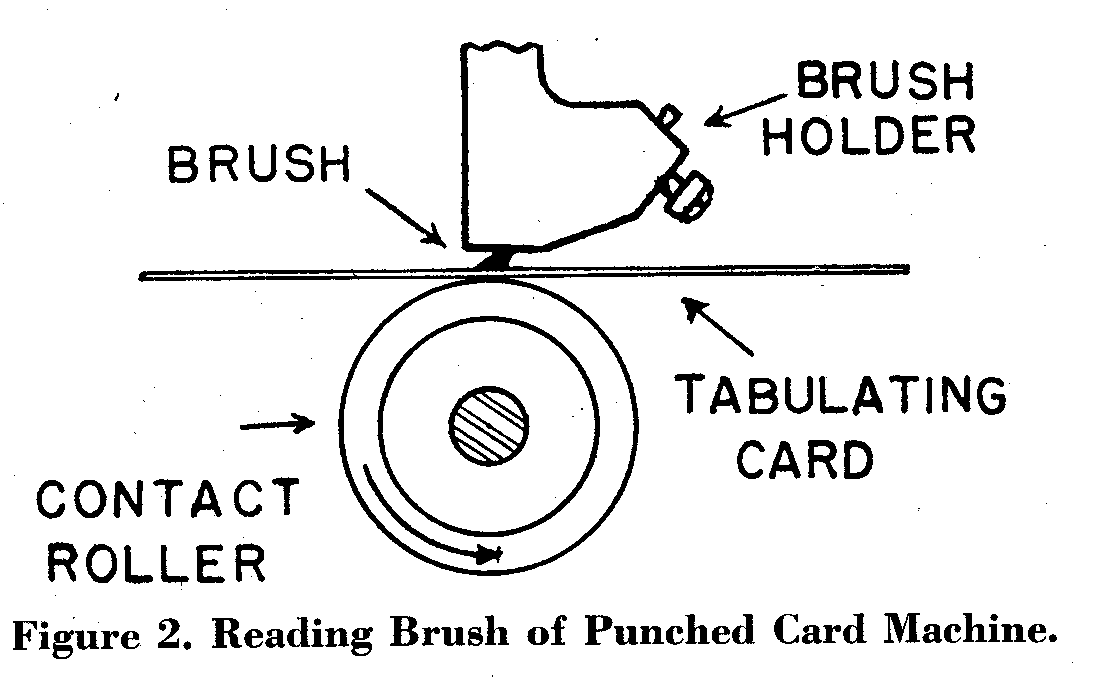 A hole punched in the card permits the brush and the roller to make contact,
thus completing an electrical circuit; the electrical impulse is made
available on a pluggable control panel, and the timing of the impulse is
determined by the position of the hole in the card. All functions of the
machine are governed by the direction of these impulses on the control
panel, and as a result of the flexibility of this panel, a large number of
operations can be performed. A large percentage of the problems encountered
in numerical computation can be handled efficiently on the standard IBM
machines. The first step in the approach to these problems is to translate
the original data into the language of the calculators. That is, to record
it in the form of punched holes on standard cards. This is the function of
the Key Punch. The desired information is transcribed onto the card by
depressing the keys on the machine in line with the appropriate column.
These cards may be fed into the Key Punch either manually or automatically.
As each column is punched, the card advances automatically to the next
punching pbsition. The numerical punches have fourteen keys; one for each
of the twelve punching positions, a space key, and a card eject key. The
alphabetical punches have, in addition, a typewriter keyboard which
automatically punches two holes per column. Having been coded by the Key
Punch, the cards are then ready for passage through any of the other
machines required for the solution of the problem.
A hole punched in the card permits the brush and the roller to make contact,
thus completing an electrical circuit; the electrical impulse is made
available on a pluggable control panel, and the timing of the impulse is
determined by the position of the hole in the card. All functions of the
machine are governed by the direction of these impulses on the control
panel, and as a result of the flexibility of this panel, a large number of
operations can be performed. A large percentage of the problems encountered
in numerical computation can be handled efficiently on the standard IBM
machines. The first step in the approach to these problems is to translate
the original data into the language of the calculators. That is, to record
it in the form of punched holes on standard cards. This is the function of
the Key Punch. The desired information is transcribed onto the card by
depressing the keys on the machine in line with the appropriate column.
These cards may be fed into the Key Punch either manually or automatically.
As each column is punched, the card advances automatically to the next
punching pbsition. The numerical punches have fourteen keys; one for each
of the twelve punching positions, a space key, and a card eject key. The
alphabetical punches have, in addition, a typewriter keyboard which
automatically punches two holes per column. Having been coded by the Key
Punch, the cards are then ready for passage through any of the other
machines required for the solution of the problem.
The Sorter is used to arrange punched cards in any desired numerical or alphabetical order depending upon the information on them. The cards to be sorted are fed from a hopper to a single brush, which reads the selected column and sorts each card into the proper one of the thirteen available pockets. There is a pocket for each of the twelve punching positions and one for blank columns. By successive sortings the cards are arranged in any desired order. The machine, which operates at a speed of 450 cards per minute, is equipped with a counter to record the number of cards passing through.
The Alphabetic Interpreter is designed to translate the numerical or alphabetical information in the card into printed figures on either of two lines at the top of the card. Thus the punched card is more easily read, and may be used as a file card as well as in the machines.
The Accounting Machine is a high-speed adding and printing machine. It reads data from a card, adds and subtracts them into counters, and prints on a sheet of paper information from the cards or totals from the counters. The machine lists alphabetical or numerical data at the rate of eighty cards a minute, or accumulates as many as eighty digits of totals at 150 cards a minute.
The Reproducing Punch transcribes all or any part of the data punched on one set of cards onto another set, or copies data from one master card onto a group of detail cards. The punch has a comparing unit which compares the two sets of data and indicates any disagreement between the two. The machine may be adapted for use as a Summary Punch to record on a new card amounts which have been accumulated in the Accounting Machine.
The Collator performs some of the functions of the Sorter in a more efficient manner. It files two sets of cards together, selects particular cards in any of four selection pockets, matches two sets of cards according to a control number, and checks the sequence of a set of cards. The machine is very flexible and permits the handling of cards according to a complicated pattern involving the comparison of two control numbers. Cards may pass through the Collator at the rate of 240 to 480 a minute.
The Electronic Calculating Punch is a high-speed machine that utilizes electronic circuits for performing all basic operations. It adds, subtracts, multiplies, and divides the numbers fed into it on a card, and punches the answers on the same card or a subsequent one. It performs these operations repetitively and in any order in a fraction of a second. The Calculating Punch reads factors punched on a card, and performs additions, subtractions, multiplications, and divisions, in any order desired. Separate results may be punched for each type of calculation, or the results may be stored and used as a factor for following computations. This machine has calculated eighth order differences of an eleven-digit function and many complicated equations involving a large number of operations.
In addition to the standard machines described above, there are at the laboratory a number of specially designed calculators which operate by means of relay networks and electronic circuits. Below is a brief description of these special machines.
The Relay Calculator performs all the basic arithmetical operations, including the determination of square roots through a complicated relay network. The extreme flexibility of this calculator is due to its large internal memory, its speed in performing computations, its ability to simultaneously read four cards and punch a fifth, and its capacity for operating under an extensive and varied program. The machine is equipped with a collating circuit to facilitate table look-up operations. A great many complicated problems have been solved on a Relay Calculator including multiplication of harmonic series, multiplication of matrices, and sixth order differential equations.
The Card-Operated Sequence Calculator consists of an Accounting Machine that reads, adds, subtracts, and stores the data, a Summary Punch that punches the final values, a relay box to provide for flexibility of control of the operations, and a unit that performs multiplications and divisions. The operations of the other calculators are usually programmed through the wiring on the control panel, while this machine has essentially one basic control panel set up and is governed by coded punches in the card. This calculator has proven to be particularly adept at computing orbits of asteroids.
The Linear Equation Solver is an electrical device for the solutIon of simultaneous linear equations up to and including the twelfth order. After coefficients of the equations have been set up on dials, switches, or punched cards, the different variables are adjusted until a solution is obtained. The method of solution is one which gives very rapid convergence. This machine was built at the laboratory by Mr. Robert M. Walker, a member of our staff, and Professor Francis J. Murray of the University's mathematics department.
The Card-Controlled Measuring and Recording Machine is designed primarily for the measurement of astronomical photographs, although it can be readily applied to photographs in any field. A photographic plate of a portion of the sky which includes the star in question is introduced into the machine together with a punched card indicating the approximate coordinates of the star. The machine then automatically reads the punched card, locates the star on the photographic plate from these approximate coordinates, accurately measures its position, and records this measurement on a card. The punched card record is then available for mathematical treatment.
Since the inception of the Astronomical Bureau in 1934, several score of other punched card laboratories have been established throughout industry and government. Those laboratories in operation during the war years played a critical part in our national defense program. In this group were the Ballistic Research Laboratories at Aberdeen, Maryland and Dahlgren, Virginia. In this same category was the U.S. Naval Observatory which prepared astronomical tables for use in air and sea navigation, astronomy and surveying. In industry, computing laboratories have assumed a prominent role in both pure and applied scientific research. Punched card techniques have been employed, for example, in the solution of problems concerned with the stress and strain analysis of aircraft structures and the vibration analysis of large machinery.
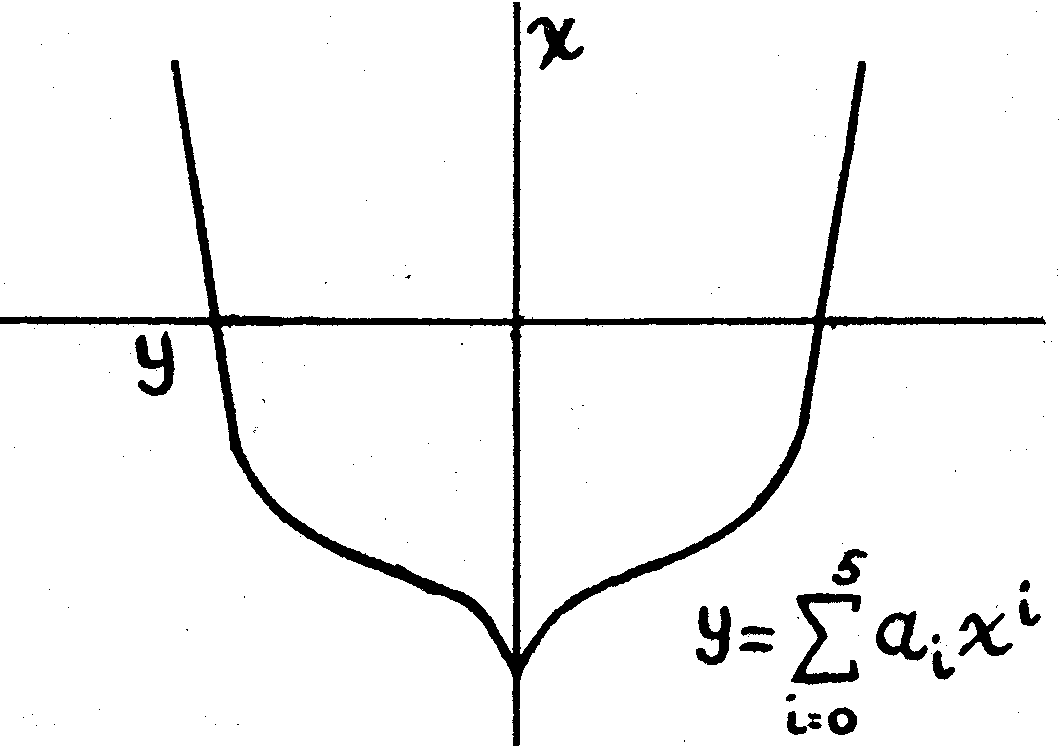
An illustration of the application of punch card equipment in problems of industry arises in the design and construction of ships, where it is necessary to specify the exact locations of a large number of points on the surface. The designer may accomplish this by considering various cross-sections through the hull and representing the outline of each of these sections by a polynomial of, say, the fifth degree (see fig. 3).
|
| Figure 3. Cross-Section Through Vessel |
Contributed by: Eleanor Krawitz Kolchin, November 2003.
Scanned and converted to HTML:
Sat Nov 22 17:06:54 2003
Converted to HTML5:
Sat Feb 23 08:52:56 2019
Also by the author:
- Krawitz, Eleanor, "Punched Card Mathematical Tables on Standard IBM Equipment", Proceedings, Industrial Computation Seminar, IBM, New York (Sep 1950), pp.52-56.
- Krawitz, Eleanor, "Matrix by Vector Multiplication on the IBM Type 602-A Calculating Punch", Proceedings, Industrial Computation Seminar, IBM, New York (Sep 1950), pp.66-70.
- Green, Louis C., Nancy E. Weber, and Eleanor Krawitz, "The Use of Calculated and Observed Energies in the Computation of Oscillator Strengths and the f-Sum Rule" Astrophysical Journal, Vol.113 No.3 (May 1951), pp.690-696.
- Green, Louis C.,, Marjorie M. Mulder, Paul C. Milner, Margaret N. Lewis, John W. Woll, Jr., Eleanor K. Kolchin, and David Mace, "Analysis of the Three Parameter Wave Function of Hylleraas for the He i Ground State in Terms of Central Field Wave Functions", Physical Review 96, 319, 15 October 1954.
- Green, Louis C., Satoshi Matsushima, Cynthia Stephens, Eleanor K. Kolchin, Majorie M. Kohler, Yenking Wang, Barbara B. Baldwin, and Robert J. Wisner, "Effect on the Energy of Increased Flexibility in the Separable Factor of Hylleraas-Type Atomic Wave Functions from H− to O VII", Physical Review 112, 1187, 15 November 1958.
- Green, Louis C.; Matsushima, Satoshi; Kolchin, Eleanor K., "Tables of the Continuum Wave Functions for Hydrogen", Astrophysical Journal Supplement, vol. 3, November 1958, p.459.
- Green, Louis C., Cynthia Stephens, Eleanor K. Kolchin, et al., "He I Ground‐State Wave Function of the Form ψ=f(r1)f(r2)g(r12)", Journal of Chemical Physics 30, 1061 (1959).
- Green, Louis C., Eleanor K. Kolchin, Norma C. Johnson, "Wave Functions for the Excited States of Neutral Helium", Physical Review 139(2A):363-378, July 1965.
- Green, Louis C., Eleanor K. Kolchin, "Equi-density surfaces in synchronously rotating close binaries built on polytropic model ν=3", Astrophysics and Space Science, Issue 2, April 1973, pp.285-288.
Links (Updated 13 February 2023):
- The Face Of A 'Computer' from 1946, Huffington Post, interview of Eleanor Kolchin by Bianca Bosker, 25 February 2013 [locally archived article text].
- "The Internal Memo That Allowed IBM's Female Employees to Get Married", The Atlantic, 4 Feb 2013 [locally archived article text].
- Association for Computing Machinery Committee on Women, 2014 National Center for Women and Information Technology Pioneer Award (Facebook, May 21, 2014, same picture as above with caption: “Eleanor Kolchin, recipient of the NCWIT 2014 Pioneer Award. She was a computer! At 88, the only person in the room (I suspect) who actually programmed with plugboards.”)
- 2014 NCWIT Eleanor Kolchin Pioneer Award (video of speech by Krawitz-Kolchin).
- Eleanor Kolchin Profile, NCWIT Boca West Special Interest Club (2014) [locally archived article text].
Translations of this page courtesy of...
| Language | Translation link | Translator | Organization |
|---|---|---|---|
| Albanian | Shqip | Armando Hysenaj | |
| Azerbaijani | Azərbaycanca | Vladyslav Byshuk | Владислав Бишук | skyclinic.ua |
| Bengali | বাংলা | shopitkart.com | |
| Bulgarian | български | Silviu Mercan | |
| Chinese (simplified) | 中文 | Vladyslav Byshuk | Владислав Бишук | studybounty.com |
| Chinese (traditional) | 繁體字 | Austin Cole | MattressMoz.com |
| Croatian | Hrvatski | Philipp Egger | Studhilfe.de |
| Czech | Čeština | Vladyslav Byshuk | Владислав Бишук | studycrumb.com |
| Danish | Dansk | (anonymous) | Clipart Library |
| Dutch | Nederlands | Lisa Kok | mrkortingscode.nl |
| Dutch | Nederlands | Justin Watson | nobulls**tseeds.com |
| Estonian | Eesti | Sonja Kulmala | University of Tartu |
| Finnish | Suomi | Fijavan Brenk | |
| French | Français | worldliterate.com | |
| Georgian | ქართული | Ana Mirilashvili | LPA Code Professional Scientific Translations |
| German | Deutsch | Kerstin Schmidt | writemypaper4me.org |
| Greek | Ελληνικά | Kerstin Schmidt | justdomyhomework.com/ |
| Hindi | हिंदी | Nikol Barton | Deals Daddy |
| Hungarian | Magyar | Zoltan Baffy | Vouchers4U.com | Indonesian | Bahasa Indonesia | Jordan Silaen | chameleonjohn.com |
| Italian | Italiano | Wall Art Shop | |
| Japanese | 日本語 | Daily Deals Coupon | |
| Lithuanian | Lietuvių | Kerstin Schmidt | pro-academic-writers.com |
| Macedonian | Македонски | Elena Simski | Unit Converter |
| Norwegian | Norsk | Lisa Kok | mrkortingscode.nl |
| Portuguese | Português | Maxwell Edward | fateknoloji.com |
| Romanian | Română | Irina Vasilescu | |
| Russian | Русский | Blue Horizon Prints | |
| Sindhi | سنڌي | Ahsan Soomro | mobilemall.pk |
| Slovenian | Slovenščina | Kerstin Schmidt | https://writemyessay4me.org/ |
| Spanish | Español | Agencia de Traduccion | |
| Swedish | Svenska | Kerstin Schmidt | https://prothesiswriter.com/ |
| Ukrainian | Українська | Olga Ponomarenko | UK Edubirdie |
| Urdu | اردو | Sharifa | RealMS |
| Uzbek | O’zbekcha | Kerstin Schmidt | https://admission-writer.com/ |


