Introduction to Earth Sciences I

2.1 Tilt, Wobble & Stretch

The Earth experiences three dominant periodic motions of much longer periods that are not readily perceptible. Each of these give insight into the interior structure of the Earth or has a direct effect on the Earth's climate because they change the basic geometry of the Earth in its orientation with respect to the Sun.

2.1.1. Axial Precession

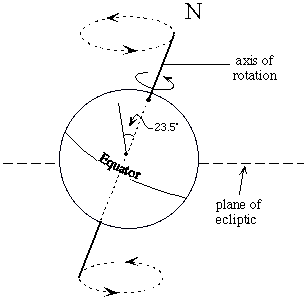
The rotational axis of the Earth is tilted with respect to the normal to the plane of the ecliptic, presently at an angle of about 23.5°. That is, it doesn't stand up straight but leans over a bit. Because of the oblate shape of the Earth and the tilt, the Sun exerts a gravitational pull that differs in force at the two poles. The effect is to attempt to set the Earth up straight - i.e., to try to right the axis to be normal to the ecliptic. This would be a least energy configuration. This "righting force" has the effect of causing the rotational axis to execute a circular, wobbling motion, like a spinning top.

Figure 2.1.1

Video resource: Axial precession video 1 (QuickTime 3MB) | Axial precession video 1 (Streamed Real Media)
Video resource: Axial precession video 2 (QuickTime ~9MB) | Axial precession video 2 (Streamed Real Media)

To understand the motion imagine a rod through the Earth's axis of rotation. Hold the rod at its middle point (the center of the Earth) and make one end move around in a circle. That's what the precession describes. The motion goes through a complete circle in a period of about 26,000 years. Why 26,000 years? This period is governed by the magnitude of the gravitational field and the tilt angle (23.5°), but also the "dynamic elipticity", H.

The dynamic elipticity is the ratio of the Earth's "moments of inertia". The concept of moment of inertia is related to the more familiar concept of inertia.

Inertia - tendency of a body to stay at rest, or retain its current motion.

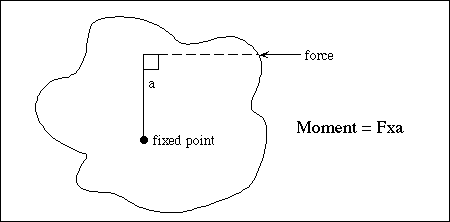
Figure 2.1.2

Moment of Inertia - tendency of a force to cause a body to rotate, or the tendency of a body to remain rotating once rotating.

Moment of Inertia must always be defined about an axis.

The Earth can be considered to have two moments of inertia - one defined about the polar axis (C); the other about an axis drawn through the equatorial plane (A).

Figure 2.1.3

The ratio is called the dynamic elipticity, and controls the rate of motion of the rotational axis in space. Remember that the ratio of axial lengths describing the Earth's shape is its elipticity and could be thought of as its static elipticity.

Considering the problem in an inverse way, if we knew the rate of motion we should be able to calculate the dynamic elipticity, H. The rate of motion is known from the "precession of the equinoxes" - the fact that over history different constellations have been visible overhead at different times in the past. At the Spring Equinox, Pisces is directly overhead at the equator, while it has been recorded that in 120 B.C. Aires was overhead at the Spring Equinox. The 26,000 year period can be estimated that way although more accurate present day calculations give a better figure.

Using 26,000 years we can deduce that

and that

where M is the mass of the Earth, and a is the equatorial radius. What does this tell us? We can also calculate moments of inertia for various bodies.

Becausefor the Earth, it is somewhere between a point and a solid. Hence it is likely that its density increases toward the center.

If we suppose that the Earth has two basic components - half being a dense core and the other half a less dense outer shell - we can also calculate moments for these bodies.

	Moment of Inertia
2	0.367
3	0.339	<------- Closer to observed
4	0.338

If , a figure appropriate for the outer shell, then - a fairly good estimate of average density of the Earth's core.

So, as in the topics we dealt with learning about the Earth's macroscopic (but static) properties we have

Observation	Theory	Deduced Property
26,000 year precession	Rotational dynamics	Internal density distribution

2.1.2 Changes in Tilt

While the inclination of the Earth's rotational axis is presently 23.5° it has moved a little in the past. Like the precession of the equinoxes that reflects the circular motion of the rotational axis, the tilt changes periodically also - from about 24.5° to 21.5° over a period of about 40,000 years. So as the rotational axis wobbles, it also tilts back and forth. This motion provides no insight into the Earth's internal properties but it turns out to be very important as an influence on the Earth's climatic changes because, as we discussed above, it is the tilt with respect to the ecliptic that gives us seasons in the first place. It follows that any change in the tilt is likely to change the nature of the seasons. It could become more winter like or more summer like depending on the tilt.

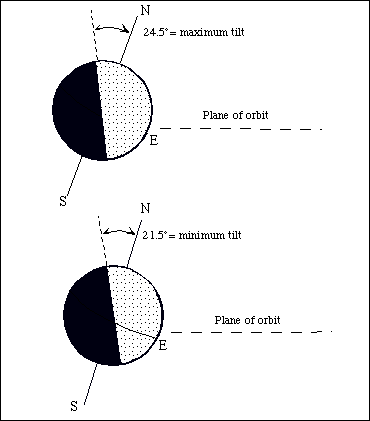
Figure 2.1.4

2.1.3 Changes in the Earth's Orbit

The Earth revolves around the Sun at a full revolution rate of 365 days. The shape of the orbit is eliptical with the Sun at one focus. This orbital state too is not static. The elipticity of the orbit changes, also in a periodic way, with this period being the longest - at around 100,000 years. The elipticity changes from 0.01 to 0.007; i.e., by 6%, quite a large amount.

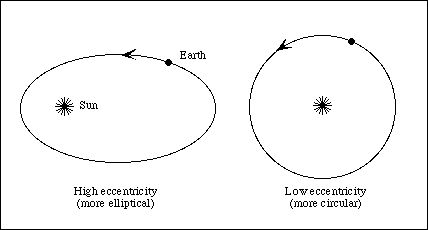
Figure 2.1.5

In summary, these three motions can be thought of as a 100,000 year stretch of the orbital ellipse, a 40,000 year tilt of the rotational axis, together with a 26,000 year wobble of the rotational axis. Wobble and stretch are actually coupled - if one changes the other is also forced to change along with it.

Next