Full Page Version | Step-by-Step version
<-->Introduction to Earth Sciences I
Topic 1
The Earth's Macroscopic Properties
and What They Can Tell Us
To get some very basic descriptions of the Earth we will start by describing some of the simplest of all the Earth's properties - how big, how heavy, how hot, how strong - and how they were deduced. The other world visitor would be remiss if he he did not at least provide a description of those properties. Most of them were deduced many years ago and represent some of the first specific inquiries into the nature of the planet we live on. Even these gross external properties can be used to infer quite a lot of information about the interior properties.
1.1 The Earth's Size and Shape
Centuries ago people had very little idea about the total size of the Earth and hardly any notion of its shape. Few people traveled very far because transportation was difficult. So the total size of the Earth became an early object of inquiry.
One of the earliest attempts to estimate the Earth's size was done by Eratosthenes about 200 B.C. His deduction was based on a curious observation (his data) that intrigued him. He lived in Alexandria but had heard that in Syene, on the longest day of the year, the sun at midday shone directly down a well without making a shadow - meaning that it was absolutely overhead at that time. He also knew that this was not true on the same day in his hometown of Alexandria, and this puzzled him a lot. His deduction allowed the size of the Earth to be estimated.

If the Earth were flat the "sun angle" would be the same everywhere. The sun is so far from the earth that the light "rays" from the sun are more or less parallel
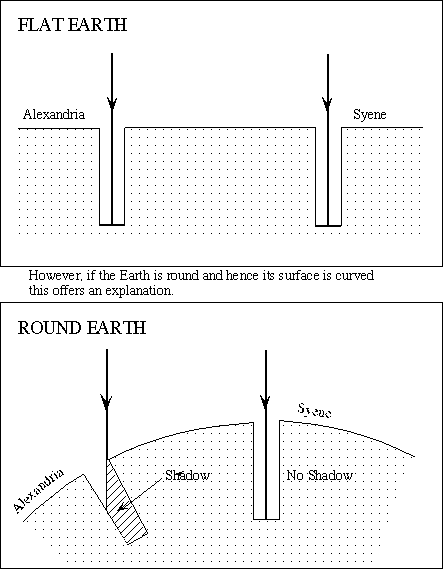
If the Earth is round then the "sun angle" would change and he reasoned that the amount of sun angle change had to have something to do with the Earth's total size. Apparently the idea that the Earth is round (spherical) was know at this time, well before Europeans made the same deduction. If it is round it has a radius and he knew how to find its radius because he knew geometry from Phythagoras.
Because of this he knew about angles. At that time the concept of "angle" was still new and it was cast in terms of ratios in two different ways.
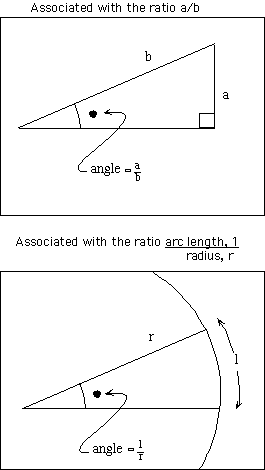
Eratosthenes measured the sun angle on the longest day at midday using the shadow cast by a vertical stick -- a triangle made by a vertical stick in the ground and the length of the shadow it cast.
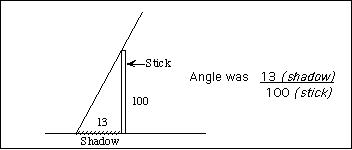
Eratosthenes used his knowledge of elementary geometry and reasoned that the angle made by the stick's shadow was the same angle as that made by the arc length from Syene to Alexandria and he knew the distance from Syene to Alexandria.
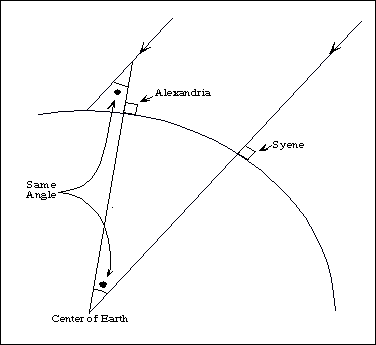
From there he could get the circumference of the Earth which he estimated at 24,500 miles, only about 50 miles off current best estimate. By dividing the angle he deduced what fraction of the circumference was represented by the distance between Syene and Alexandria. Other descriptions of Eratosthenes' famous experiment can be found at http://www.algonet.se/~sirius/eaae/aol/market/collabor/erathost/ and http://share2.esd105.wednet.edu/jmcald/Aristarchus/eratosthenes.html.
Mini-Quiz:
Forward and Inverse Thinking
Relating what Erastosthenes did to the ideas in our opening comments, we would say that the data available to Erathosthenes was the curious observations of shadows in wells and sticks. He then used a theory of angles, to infer one of the Earth's critical parameters - its radius - which he could not measure directly.
Viewed as an inverse problem, the data and theory of angles were used to deduce an important size parameter.
Viewed as a forward problem, the radius parameter and theory can be used to explain the shadow problems.
Shape of the Earth
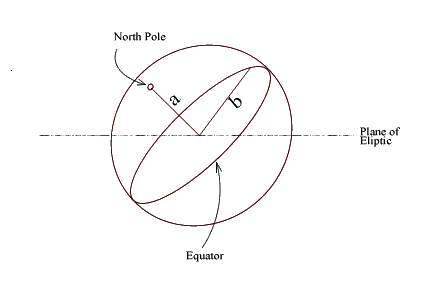
What Erastosthenes couldn't know is that the Earth is actually oblate; its equatorial radius being greater than the polar radius. This took many more years of very accurate geodetic measurements and the shape of the Earth has only been determined with any significant accuracy in the 20th century.
The Earth departs from a purely spherical shape in having an equatorial radius that is greater than its polar radius.
![]()
The same number for the Moon is about ![]() . The Moon is more nearly
spherical. The oblate shape of the Earth is prima faci evidence that it is not
completely solid throughout. That it bulges at its equator suggests that it
must be somewhat liquid-like. If we were to spin a water-filled balloon on a
Potter's wheel it would bulge out - that's essentially what the Earth does.
If you were to spin a balloon at the same rate of spin, but filled with maple
syrup it would still bulge out but by a smaller amount. For any particular fluid
in the balloon, the faster you spun it the more it would bulge. Even a solid
sphere spun fast enough will budge a bit. Because the Moon does not do have
the same extent of bulge as the Earth suggests that it is more nearly solid.
In fact the Moon presents the same face to the Earth and is not rotating on
its axis like the Earth. The Moon's elliptically is a relic feature from a time
when it was less solid and rotating. Earth's elipticity is part relic, part
dynamic.
. The Moon is more nearly
spherical. The oblate shape of the Earth is prima faci evidence that it is not
completely solid throughout. That it bulges at its equator suggests that it
must be somewhat liquid-like. If we were to spin a water-filled balloon on a
Potter's wheel it would bulge out - that's essentially what the Earth does.
If you were to spin a balloon at the same rate of spin, but filled with maple
syrup it would still bulge out but by a smaller amount. For any particular fluid
in the balloon, the faster you spun it the more it would bulge. Even a solid
sphere spun fast enough will budge a bit. Because the Moon does not do have
the same extent of bulge as the Earth suggests that it is more nearly solid.
In fact the Moon presents the same face to the Earth and is not rotating on
its axis like the Earth. The Moon's elliptically is a relic feature from a time
when it was less solid and rotating. Earth's elipticity is part relic, part
dynamic.
This oblateness, combined with the inclination of the rotational axis with respect to the plane of the ecliptic (the plane that contains the Sun and in which most of the planets revolve around the Sun), governs much of the planetary dynamics as we will see later on in Topic 2 of these lectures.
The shape of the Earth is now known in great detail primarily from satellite observations. The Earth departs from spherical in many important ways and this results in the mass of the Earth being unevenly distributed. This too governs the planetary motion. Imagine how a basketball would spin in space if you glued a small weight on one part of the exterior. It would wobble as it spun. If the mass were moved around in a more uniform manner the period of rotation would change. We will learn about how the Earth rotates in the lectures under the second topic.
In fact, the Earth's period of rotation does change regularly by a few milliseconds (thousandths of a second). Accurate measurements of the length of the day (the rate of rotation) show that the rotation period changes with the seasons as water is redistributed over the Earth and the relative amounts of ice, water and water vapor varies. The effect of an El Nino can be seen in changes of the length of day. Human activity also changes the rotation period -- when the Three Gorges Dam in China is filled the change in length of day will discernible to a skilled amateur astronomer.
Mini-Quiz:
1.2 Mass of the Earth: Cavendish's Experiment to "Weigh the Earth"
The next thing is to try to find out how much the Earth might weigh. This is much more difficult, and requires a very cunning experiment.
The first attempt to do this was made by Cavendish in 1798. Again the elements of theory, observation and deduced quantity are present. In this case we begin with Newton's universal law of gravitation which describes the force of attraction between two bodies having mass, and use the theory to set up an experiment that will allow the Earth's mass to be determined -
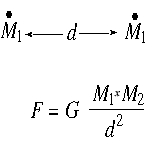
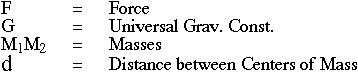
Even though the masses have real shapes, their attraction to one another would be the same as if all the mass were concentrated at a point -- the so-called "center of gravity" or "center of mass".
With this simple formula, Cavendish established the mass of the Earth using a very accurate balance beam by the following steps -
![]()
|
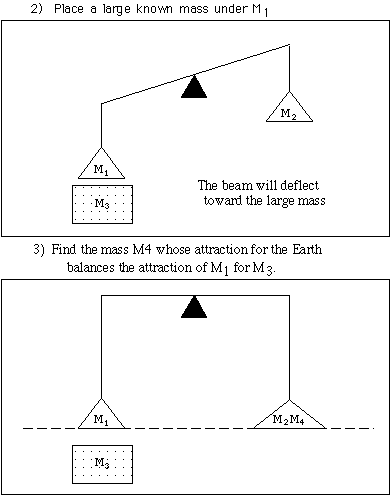
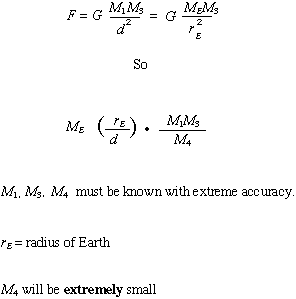
![]()
![]()
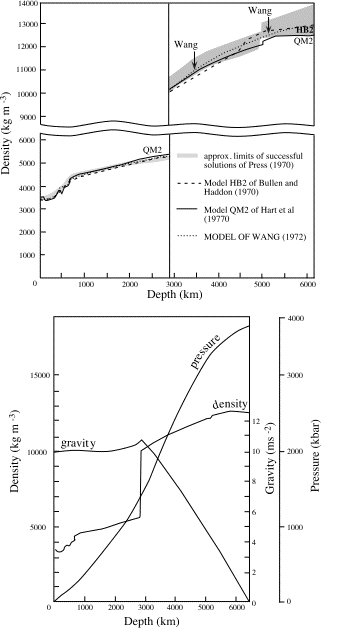
The exact density profile of the Earth is not well known, but the best estimates come from seismic studies. Seismic energy from earthquakes penetrates the whole Earth and allows us to determine the internal structure based on the speed of propagation of energy (we will deal with this in a later section). The speed of propagation is related to density in a regular way so that allows the density structure to be deduced.
Mini-Quiz:
1.3 The Earth's Strength
Although it is a fundamental quantity of any material object, the question, "how strong is the Earth" was not really addressed very closely until fairly recently. The answer, it would seem on first thought, is that it is almost infinitely strong - at least the rocky parts of the continents. For most common purposes, the Earth is indeed very strong. However, we are fairly confident that the Earth's (outer) core is liquid and that volcanic rocks rise from deep in the Earth so we know that it is not completely rigid through and through. We also know from the bulging middle shape that it must be somewhat soft in gross properties. How can we get an idea of the Earth's strength? There are several ways and in each we have to analyze experiments the Earth is performing on itself.
1.3.1. The Earth Rings Like A Bell
Given a sufficiently large earthquake, like the Good Friday earthquake in Alaska in 1964, which had a magnitude of 8.6, the entire Earth actually vibrates. It is fairly intuitive that the amplitude and "tone" of the vibrations must relate in some way to the material properties of the Earth. Imagine three tuning forks, one made of aluminum, one of steel and one of titanium, each struck equally hard. The pitch of individual tuning forks will be different and the time it takes for the tone to die away will differ also. The aluminum fork will make a dull thud and the sound will die out quickly; the titanium fork will make a high pitched ring and vibrate for a long time.
In the Earth these vibrations are called "normal modes" or "free oscillations." The normal mode period for a solid iron ball as large as the Earth can be calculated. In 1911 A.E.H. Love made the calculations and determined the period would be about an hour. That is, struck hard enough the whole Earth would vibrate in and out every hour. In 1954 Hugo Benioff announced that he thought he had detected a normal mode of 57 minutes from the Kamchatka earthquake of that year, but the first real proof came in 1961 by Bruce Bolt who clearly identified a 54 minute mode associated with the 1960 Chilean earthquake. He also saw much shorter period vibrations that represent harmonics or overtones of the fundamental long period mode.
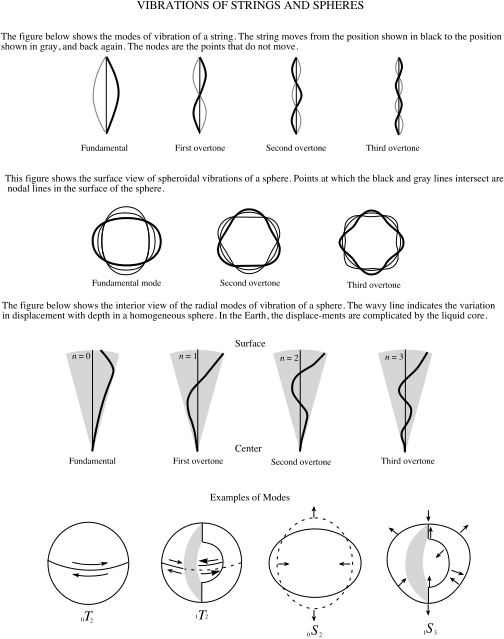
The fundamental mode vibrations can tell us about the properties of the whole Earth. The harmonics or overtones give us insight into the deeper parts of the Earth. It is usual to calculate on a computer the expected harmonics for various Earth structures and compare them to observations. That is, the process follows a forward approach. Normal mode inverse methods are available also but they are difficult to implement.
As we started off at the beginning, we can think of this in terms of information types - we observe normal mode vibrations and using a theory of elasticity we can infer parameters associated with the Earth's strength.
1.3.2. The Earth Responds To The Moon - Earth Tides
While it might seem incredible, the Earth as a whole responds to the pull of the Moon's gravity. The moon is, of course, responsible for the ocean tides (and we will study these a little later in topic 2) but its gravitational pull is strong enough to distort the shape of the solid Earth also. The Earth's surface actually rises up a little when the moon is overhead. While the ocean tides have a range of several tens of feet in places and are commonly several feet, the surface of the solid earth moves only about 10 cm at most; much less in many places.
Obviously the moon is exerting the same pull on the oceans as it is on the solid earth, and the amount it yields is a measure of the strength of rock compared to water. In the same way, as we described for normal modes, we can calculate the yielding that would be associated with a fully rigid Earth and one with yeilding. It is therefore possible to determine just how soft the center is by matching predictions and observations.
The distortion is described by so-called Love numbers after the same A.E.H. Love who studied normal modes. These Love numbers are a measure of the Earth's yield strength.
1.3.3. The Earth Bends When A Weight Is Placed On It
We can learn a lot about the strength of materials by the way they bend. Our instinct is always to try to distort an object to get a sense of how strong - resistant to forces - it is. When we squeeze melons at the fruit stand to make sure they are not over ripe we are measuring their strength, knowing that they get soft if they are too ripe.
We cannot really do that for the Earth other than in samples of rocks from near the surface from which we learn that most crustal rocks are indeed very strong. We build buildings out of rocks. Fortunately the Earth has performed some bending experiments for us that can be used for this purpose.
Volcanic Islands -
The color map below shows the shape of the Pacific
ocean floor around the Hawaiian Islands. The image was created by a software
tool that can be accessed at http://www.ldeo.columbia.edu/dees/ees/lithosphere/index.html.
This is the site that supports one section of the course for Earth Science concentrators.
Click on the image in the upper right and use the Zoom function to home in on
different parts of the world. Just click on the image to re-center the map.
The brown and yellow colors show elevation above sea level and the blue green
colors are depths below sea level. You see the chain of the Hawaiian Islands
with the "Big Island" to the southeast in brown shades. Look closely
around the islands and you will see that the ocean gets quite deep immediately
adjacent to the islands as you might expect. But there is also a diffuse halo
of shallower ocean floor around the island chain. The black and white figure
below shows a cross section through the main island.
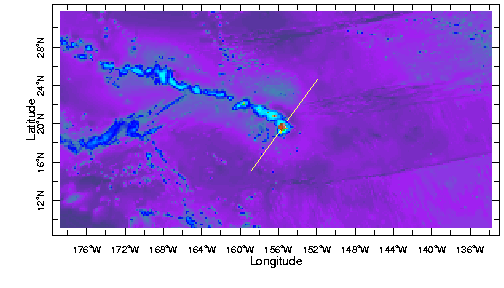
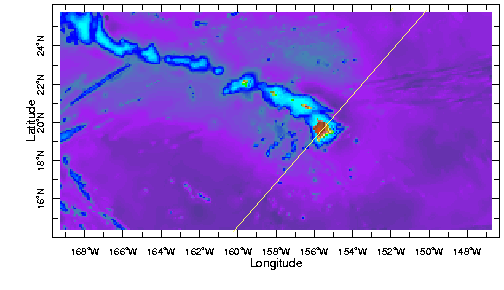
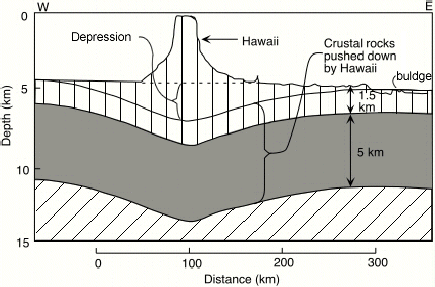
The formation of a volcano involves the transfer of a very large amount of molten material from deep in the Earth to the surface. Lava erupts at the surface and builds up in a pile that is extremely heavy. The weight presses down on the Earth's surface and, if the volcano is large enough, will cause the layers beneath to bend downward. This process is very apparent in the Hawaiian Islands where the weight of the newly forming islands is pushing the layers beneath downward. This means that the layers must have finite strength or they would carry the load without changing shape. The amount by which the underlying layers bend is a measure (indirect) of their strength - the more they bend the weaker they are.
In fact, almost all the islands in the Pacific Ocean show evidence that they are bending the layers beneath. Bending seems to be greater in some places than others but the shape always seems to be much the same - a depression around the island and a bulge further out. This depression and bulge shape tells us that the layers beneath are deforming in an elastic manner. By this we mean that if the weight were removed the Earth would spring back (slowly) to its original shape. It is the size of the depression and the distance from the islands to bulge that tells us the strength, or rigidity, as it is usually stated.
When we look at these strength measures from islands in the Pacific we find there are systematic patterns. The layers are weaker near to mid-ocean ridge spreading centers (more on this later) and stronger further away. What we are seeing is that the Earth's outer layers get stronger as they get older - basically, they freeze harden.
Mini-Quiz:
Massive Ice Sheets -
Above we noted that the weight of volcanoes can be used to give a measure of the Earth's strength which is an elastic property. Removing the weight would cause the Earth to return to its original shape.
The Earth has also done this experiment. During the last ice age huge ice sheets covered much of Europe and North America. Manhattan was under about a mile of ice. Their weight depressed the crust beneath just as Hawaii depresses the crust. As the current inter-glacial period began about 10,000 years ago, the ice sheets melted and retreated back to their present position. In doing so they released a massive weight from the Earth. That weight had depressed the layers beneath as it presently does in Greenland and Antarctica where the rock surface beneath the ice is actually well below sea level.
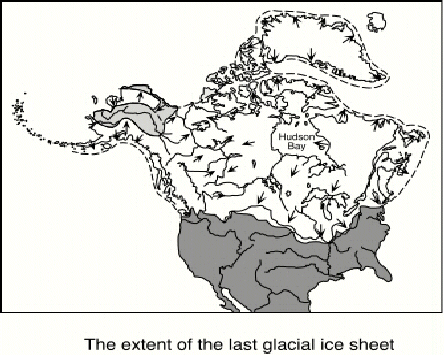
When the ice sheets were present the Earth was depressed; as they left the Earth was uplifted. But they did not rebound instantaneously. They rebounded slowly as the deep layers flowed beneath. The rate of uplift - fast or slow - is a measure of the ability of the deep layers to flow.
Basically, when the weight depresses the outer layers of the Earth, deeper layers have to flow outward to accommodate the layers, squeezing them for space. When the weight is released the deep layers flow back. The rate of flow measures the viscosity of the deep layers.
The best evidence we have for this flowing of deep layers is the uplift in Fennoscandia. We know the land is moving upward because we can see evidence for beach deposits in layers high above sea level. Because these can be dated we can measure the rate of uplift and this is a fairly direct measure of the rate of flow of the layers beneath.
Mini-Quiz:
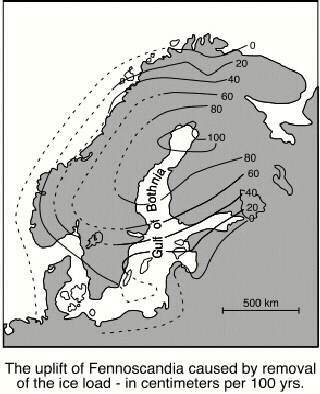
What is found from these studies is that the deep layers of the Earth must be quite fluid-like on time scales of several tens to hundreds of thousands of years. The outer surface is rigid, but beneath there is a region where the layers can flow relatively readily. This property of the Earth becomes key to understanding the global process of plate tectonics that both Professor Langmuir and I discuss. The outer rigid layer is called the lithosphere (lithos meaning rock) and the layers below capable of flow are called the asthenosphere.
1.4 Summary
We have learnt how several important macro-scale properties of the Earth were deduced. These provide a very basic description of the object we are dealing with and might represent some of the first entries made under "Earth" in the encyclopedia. In each case a set of observations were used in combination with a theory to infer the information we sought.
Information Available |
Theory |
Information Obtained |
Shadows (sun angle) in different locations |
Geometry |
Size of Earth |
Masses on balance beam |
Gravitation |
Mass of Earth, denser in middle |
Normal Mode frequencies |
Elasticity |
Strength of whole Earth |
Deformation caused by volcanic islands |
Elasticity of rigid bodies |
Strength of outer layers |
Rebound after de-glaciation |
Flow in viscous materials |
Viscosity of deep layers |
What we have deduced from these studies is that although the Earth is indeed very rigid in its outer layers, it is surprisingly soft in its inner layers. This inner softness is a critical feature of the Earth that governs many of its dynamic properties, and these are the subject of the next several topics.
To Topic 2 / To Topic 3 / To Topic 4 / To Topic 5