Problem Set
Graphing Linear Functions
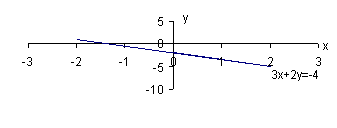
1. Graph the function 3x + 2y = -4
Solution:
Step 1. Rewrite in the form y = a + bx and simplify
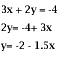
Step 2. Find a set of points which satisfy the equation and plot them.
let x = 0
then 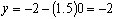
let x = 2
then 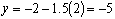
let x = -2 then
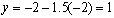
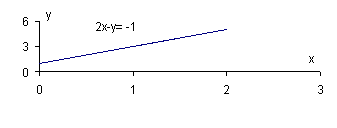
2. Graph the function 2x –y = -1
Solution:
Step 1. Rewrite in the form y = a + bx and simplify
y = 1 + 2x
Step 2. Find a set of points which satisfy the equation and plot them.
let
x = 0 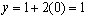
let
x = 2 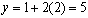
let
x = 1 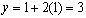
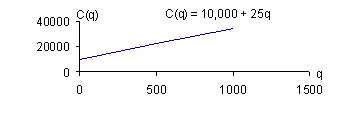
3. A copy shop can produce a course reader at a cost of $25 per copy. The monthly fixed costs are $10,000.
a. Determine the total monthly cost as a function of the number of copies produced.
b. Graph the total monthly cost function.
Solution:
a. Total cost = fixed cost + variable cost
C(q) = 10,000 + 25 q
b. Find a set of points which satisfy the equation and plot them
|
q |
C(q) |
|
0 |
10,000 |
|
100 |
12,500 |
|
500 |
22,500 |
|
1,000 |
35,000 |
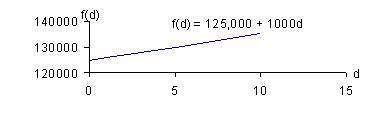
4. A chemical plant was found to be discharging toxic waste into a waterway. The state in which the chemical plant was located fined the company $125,000 plus $1,000 per day for each day on which the company continued to violate water pollution regulation.
a. Express the total fine as a function of the number of days in which the company remains in non-compliance.
b. Graph the relationship.
Solution:
a. Let d = the number of days in which the company remains in non-compliance
f(d) = 125,000 + 1000d
b. Find a set of points which satisfy the equation and plot them
|
d |
f(d) |
|
0 |
125,000 |
|
1 |
126,000 |
|
5 |
130,000 |
|
10 |
135,000 |
[Index]