Deuterium Isotope Effects for Probing
Aspects of the Interaction of H–H and C–H Bonds with Transition
Metals
Introduction
It is well known that the measurement of kinetic
deuterium isotope effects (i.e. kH/kD) provides a useful means to ascertain details of the
nature of the transition state for the rate determining step of a reaction that
involves cleavage of an X–H bond. However, since many reactions are multistep, the observed
kinetic isotope effect often represents a composite of the individual isotope
effects for all steps (both forward and reverse) up to, and including, the rate
determining step. Therefore, an
understanding of equilibrium deuterium isotope effects is of importance for the
interpretation of kinetic deuterium isotope effects. Deuterium isotope effects are often rationalized by using
two guidelines, namely:
(i) Primary kinetic isotope effects (KIEs) are typically
normal (kH/kD > 1).
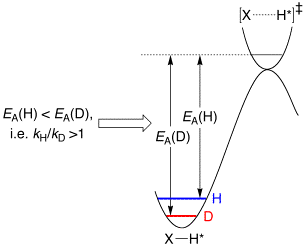
(ii) Primary equilibrium isotope effects (EIEs) may be either normal (KH/KD > 1) or inverse (KH/KD < 1), with a value that is dictated by deuterium preferring to be located in the highest frequency oscillator.
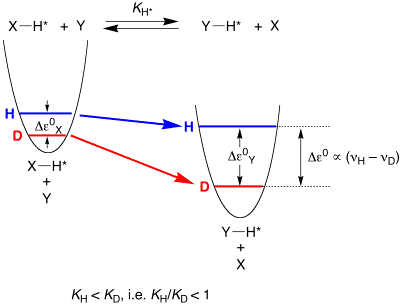
We are interested in investigating the generality of these rules as they apply to the various interaction of H–H and C–H bonds with transition metal centers.
Equilibrium Isotope Effects for Oxidative Addition of
Dihydrogen
1. An
Inverse Equilibrium Isotope Effect for Oxidative Addition of H2 to
W(PMe3)4X2
Rather surprisingly, prior to 1993, there had been no
detailed discussion in the literature pertaining to the equilibrium isotope
effect for the oxidative addition of H2 to a metal center. For this reason, we directed effort
towards establishing the EIE for oxidative addition of H2 and D2
to a metal center, and specifically W(PMe3)4I2.
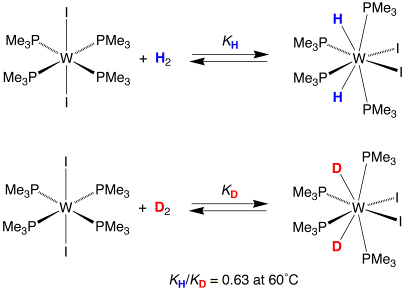
Interestingly, the equilibrium isotope effect for oxidative addition of H2 and D2 to W(PMe3)4I2 is characterized by a substantial inverse equilibrium deuterium isotope effect, with KH/KD = 0.63(5) at 60ŻC. In particular, the inverse nature of the equilibrium isotope effect is counter to that which would have been predicted on the basis of the simple notion concerning primary isotope effects, namely that deuterium prefers to reside in the higher frequency oscillator.
Analysis of the temperature dependence of K reveals that the origin of the inverse equilibrium deuterium isotope effect is enthalpic, with oxidative addition of D2 being more exothermic than oxidative addition of H2. The entropic contribution to the equilibrium isotope effect is small, but actually attempts to counter the inverse nature.
A more complete analysis of isotope effects, however,
focuses on factors other than the ZPE term. Specifically, equilibrium isotope effects are conventionally
determined by the expression EIE = SYM •
MMI • EXC •
ZPE where SYM is the symmetry factor, MMI is the mass-moment of inertia term,
EXC is the excitation term, and ZPE is the zero point energy term, an approach
that has been applied by others in organometallic
chemistry.
It is convenient to recognize that the combined [SYM•MMI•EXC]
term corresponds closely to the entropy component, while the ZPE term
corresponds closely to the enthalpy component. Most commonly, the ZPE term dominates the EIE, which is the
reason why the direction of the EIE can be predicted on the basis of
vibrational frequencies alone.
Specifically, since the difference in X–H and X–D zero point
energies scales with nX–H,
the zero point energy stabilization for a system is greatest when deuterium
resides in the highest frequency oscillator. Thus, a normal EIE is predicted if nY–H in the product is less than nX–H in the reactant, while
an inverse EIE is predicted if nY–H
in the product is greater than nX–H
in the reactant.
On this basis, a normal EIE would have been expected for
oxidative addition of H2 and D2 to W(PMe3)4I2
because the H–H stretch is of much higher energy that the W–H
stretch and one customarily focuses on stretching vibrations when evaluating
primary isotope effects. Since
this prediction is counter to the experimental result, it was evident that this
simple appraisal did not provide an accurate evaluation of the EIE for
oxidative addition of H2.
The inverse EIE may, however, be rationalized if bending modes associated with the dihydride moiety are included. Although bending modes are of sufficiently low energy that they are not normally invoked when discussing primary isotope effects, the fact that there are four such modes associated with the [WH2] moiety means that, in combination, they may provide an important contribution.
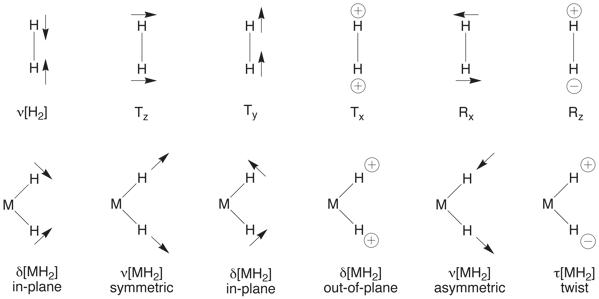
Inclusion of the bending modes results in a significant lowering of the zero point energy for W(PMe3)4D2I2 with respect to W(PMe3)4H2I2, to the extent that an inverse equilibrium isotope effect is obtained. The occurrence of an inverse deuterium equilibrium isotope effect is, therefore, a consequence of there being a single isotope sensitive vibrational mode in the reactant (H2), yet six (albeit lower energy) isotope sensitive modes in the product.
2.
Inverse to Normal Temperature Dependent Transitions for Equilibrium
Isotope Effects Involving Oxidative Addition of Dihydrogen
While inverse EIEs have become a commonly accepted feature for oxidative addition of H2 and D2 to a metal center, literature reports that coordination of alkanes to a metal center can be characterized by both normal and inverse EIEs, the possibility that oxidative addition of H2 to a single metal center could also be characterized by a normal EIE deserved further consideration. To examine this possibility, the EIE for oxidative addition of H2 and D2 to {[H2Si(C5H4)2]W} was calculated as a function of temperature.
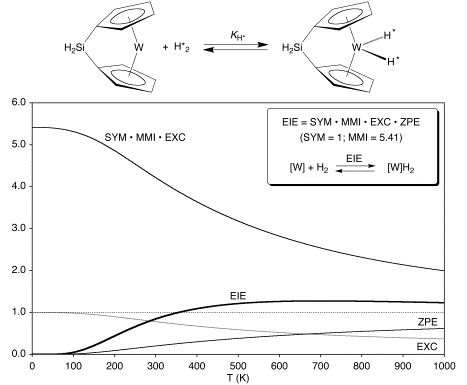
Interestingly, the calculations predicted that the EIE for oxidative addition of hydrogen to {[H2Si(C5H4)2]W} does not vary with temperature in the simple monotonic manner predicted by the van’t Hoff relationship, for which the EIE would be expected either to progressively increase or decrease and exponentially approach unity at high temperature. Rather, the EIE exhibits a maximum, being inverse at low temperature and normal at high temperature.
The precise form of the temperature dependence of the EIE is determined by the values of the individual SYM, MMI, EXC and ZPE terms. Since the SYM and MMI terms are temperature independent, the occurrence of a maximum is a result of the ZPE and EXC terms opposing each other. It is, however, more convenient to analyze the temperature dependence of the EIE in terms of the combined [SYM•MMI•EXC] term and the ZPE term, which respectively correspond to the entropy and enthalpy terms. Thus, at all temperatures the [SYM•MMI•EXC] entropy component favors a normal EIE, while the ZPE enthalpy component favors an inverse EIE. At high temperatures, the [SYM•MMI•EXC] entropy component dominates and the EIE is normal, while at low temperatures the ZPE enthalpy component dominates and the EIE is inverse.
The notion that an inverse-to-normal transition of the
EIE could be a general phenomenon was confirmed by calculating the temperature
dependence of the EIE for oxidative addition of H2 and D2
to Ir(PH3)2(CO)Cl.
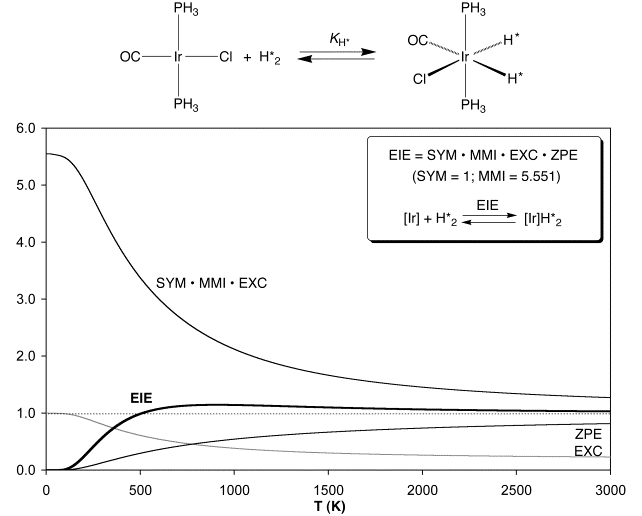
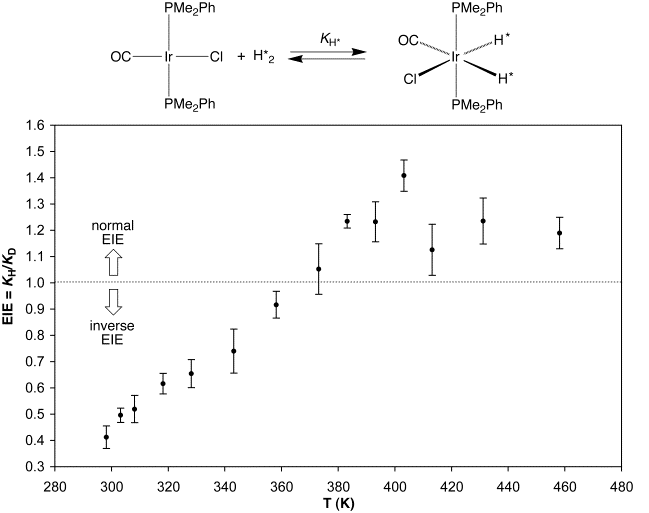
Experimental verification of the prediction that the EIE for oxidative addition of H2 to a transition metal center could undergo a temperature dependent transition from an inverse to a normal value was obtained by investigation of oxidative addition of H2 and D2 to Ir(PMe2Ph)2(CO)Cl. Thus, the strongly inverse EIE of 0.41(4) observed for oxidative addition of H2 and D2 to Ir(PMe2Ph)2(CO)Cl at 25ŻC becomes normal at temperatures greater than ca. 90ŻC, and reaches a maximum value of 1.41(6) at 130ŻC, thereby providing important verification for the theoretical calculations.
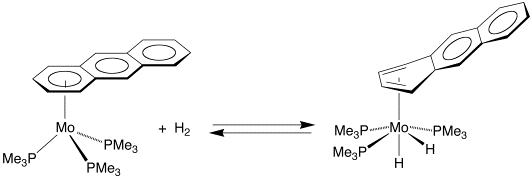
Shortly after demonstrating that oxidative addition of H2 and D2 to Ir(PMe2Ph)2(CO)Cl undergoes a transition from inverse to normal at high temperatures, a system was discovered for which the EIE for oxidative addition to a single metal center is normal at relatively low temperature (40 ŻC). Specifically, the EIE for oxidative addition of H2 and D2 to the anthracene complex (h6–AnH)Mo(PMe3)3 (AnH = anthracene) giving (h4–AnH)Mo(PMe3)3H2 is normal over virtually the entire temperature range (30 – 90ŻC) measured.
The important issue to address is concerned with the factors that influence the temperature of the inverse/normal EIE transition. Calculations on a variety of systems shows that the transition temperature is a sensitive function of the system such that some systems may exhibit a normal EIE, whereas others exhibit an inverse EIE. The main factors responsible for influencing the transition temperature are the M–H stretching frequencies such that systems for which nM–H are low are more likely to exhibit a normal EIE than systems for which nM–H are high.
As noted above, primary isotope effects are often rationalized in terms of ZPE arguments using the concept that deuterium prefers to be located in the highest frequency oscillator. On this basis, the observation of a normal isotope effect for oxidative addition of H2 to (h6–AnH)Mo(PH3)3 could have simply been interpreted in terms of the two Mo–H stretching frequencies of (h4–AnH)Mo(PH3)3H2 being lower than that of the H–H stretching frequency. However, such an analysis would be incorrect because the ZPE term actually favors an inverse EIE at all temperatures and the occurrence of a normal EIE is purely a consequence of the [SYM•MMI•EXC] (entropy) term. The important feature of (h4–AnH)Mo(PH3)3H2 which results in a normal EIE at relatively low temperatures is that the M–H vibrational modes are of low energy and cause the ZPE term to approach unity rapidly. Thus, the [SYM•MMI•EXC] entropy term is able to dominate the EIE at a relatively low temperature, thereby resulting in a normal EIE for oxidative addition of H2 to (h6–AnH)Mo(PH3)3.
3. Equilibrium Isotope Effects for Coordination of
Dihydrogen
In addition to the majority of EIEs for oxidative addition of H2 and D2 being inverse at ambient temperature, the EIEs for formation of dihydrogen complexes are also inverse. However, on the basis of the above studies, we considered the possibility that the EIE for coordination of dihydrogen could also exhibit a similar behavior. Indeed, calculations on the pentacarbonyl complex W(CO)5(h2–H2), a close relative of the first dihydrogen complexes, M(CO)3(PR3)2(h2–H2) (M = Mo, W; R = Pri, Cy), demonstrate that the EIE would become normal at higher temperatures.
Isotope Effects Pertaining to the Interaction of
Transition Metals with C–H Bonds
1.
Experimental Measurement of Isotope Effects for Reductive Elimination of
Methane from [Me2Si(C5Me4)2]W(Me)H
The kinetic isotope effect for reductive elimination of methane from [Me2Si(C5Me4)2]W(CH3)H and [Me2Si(C5Me4)2]W(CD3)D is characterized by a substantial inverse KIE of 0.45(3) in benzene at 100ŻC.
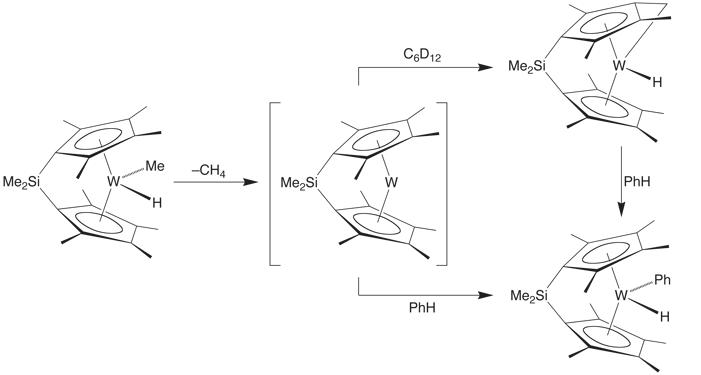
Although a normal KIE may have been expected since this has a substantial primary component, the inverse value may be readily rationalized by recognizing that the reductive elimination reaction is not a single step, but is rather a two step sequence involving formation of a s–complex intermediate [Me2Si(C5Me4)2]W(s–MeH) prior to rate-determining elimination of methane.
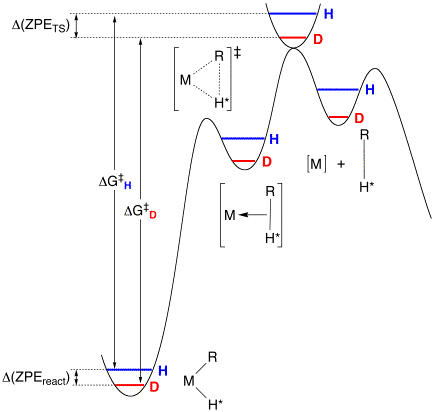
Specifically, for a situation involving a s–complex intermediate, the rate constant for irreversible reductive elimination is a composite of the rate constants for reductive coupling (krc), oxidative cleavage (koc), and dissociation (kd), namely kobs = krckd/(koc + kd). The latter expression simplifies to kobs = krckd/koc = Kskd, where Ks is the equilibrium constant for the conversion of [M](R)H to [M](s–RH) if methane dissociation is rate determining, i.e. kd << koc. If the isotope effect for dissociation of RH (i.e. [kd(H)/kd(D)]) is close to unity (since the C–H bond is close to being fully formed), the isotope effect on reductive elimination would then be dominated by the equilibrium isotope effect Ks(H)/Ks(D) for formation of the s–complex [M](s–RH). The latter would be predicted to be inverse on the basis of the simple notion that deuterium prefers to be located in the higher frequency oscillator, i.e C–D versus M–D. As such, an inverse KIE may result for the overall reductive elimination, without requiring an inverse effect for a single step. Indeed, this explanation has been invoked in the literature to rationalize inverse KIEs for a variety of systems.
However, while the preequilibrium mechanism provides a commonly accepted rationalization of inverse kinetic isotope effects for reductive elimination of RH, consideration must be given to the possibility that it could also correspond to the isotope effect for the reductive coupling step if that were to be rate determining. Since there is relatively little information pertaining to the individual isotope effects for the reductive elimination step, we considered it worthwhile to investigate this system in more detail. Although it is not possible to address this issue by studying the kinetics of reductive elimination of [Me2Si(C5Me4)2]W(CH3)H and [Me2Si(C5Me4)2]W(CD3)D, it is possible to address the issue by studying the elimination of CH3D from [Me2Si(C5Me4)2]W(CH3)D and [Me2Si(C5Me4)2]W(CH2D)H. Specifically, [Me2Si(C5Me4)2]W(CH3)D is observed to isomerize to [Me2Si(C5Me4)2]W(CH2D)H via the s–complex intermediate [Me2Si(C5Me4)2]W(s–CH3D) on a time-scale that is comparable to the overall reductive elimination of CH3D, and a kinetics analysis of the transformations permits the KIE for reductive coupling to be determined.
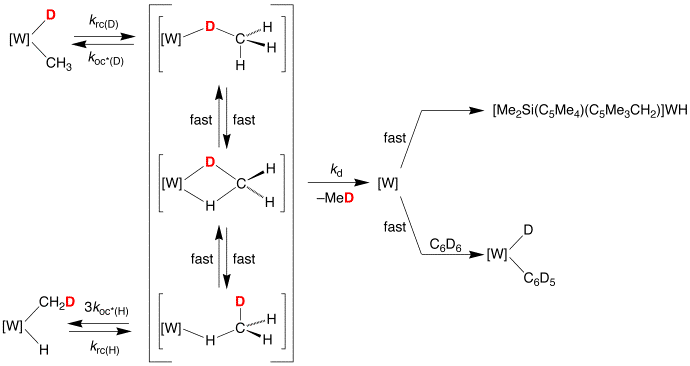
Significantly, assuming that secondary effects do not
play a dominant role, the primary KIE for reductive coupling of [Me2Si(C5Me4)2]W(Me)X
(X = H, D) to form the s–complex
intermediate [Me2Si(C5Me4)2]W(s–XMe) is normal, with a value of 1.4(2). As such, the observation of an inverse kinetic isotope
effect for the overall reductive elimination can only be rationalized in terms
of an inverse equilibrium isotope
effect for the formation of the s–complex. In this regard,
Jones has also demonstrated that the EIE for the interconversion of
[TpMe2]Rh(L)(Me)X and [TpMe2]Rh(L)(s–XMe) is inverse
(0.5), even though the individual KIEs for oxidative cleavage (4.3) and
reductive coupling (2.1) are normal.
Therefore, at present, there is no
experimental evidence which supports the notion that the inverse KIEs for
reductive elimination of methane may be attributed to an inverse primary KIE
for a single step.
2.
Equilibrium Isotope Effect for Coordination of Methane to {[H2Si(C5H4)2]W}
In addition to coordination of dihydrogen exhibiting a temperature dependent transition between inverse and normal EIEs, coordination of methane exhibits a similar behavior. Specifically, the EIE for coordination of CH4 and CD4 to {[H2Si(C5H4)2]W} exhibits a maximum: the EIE is 0 at 0 K, increases to a maximum value of 1.57, and then decreases to unity at infinite temperature.
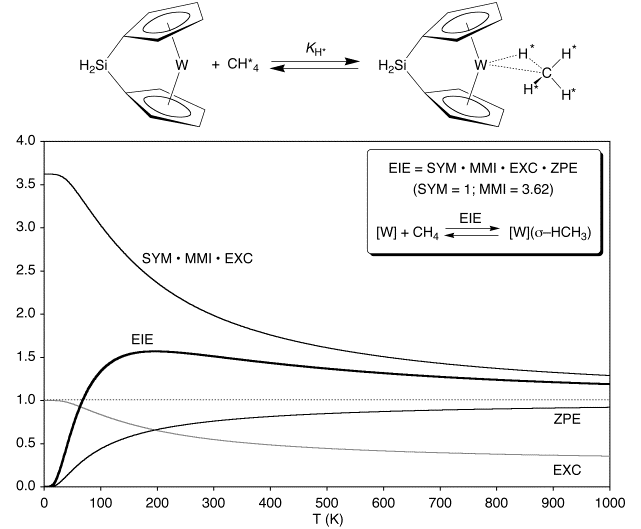
Although there are no experimental reports of the EIEs for coordination and oxidative addition of methane to a metal center for comparison with that for {[H2Si(C5H4)2]W}, there are several conflicting reports of EIE’s for coordination of other alkanes. Specifically, Geftakis and Ball reported a normal EIE (1.33 at –93ŻC) for coordination of cyclopentane to [CpRe(CO)2], whereas Bergman and Moore reported inverse EIEs for the coordination of cyclohexane (Ň 0.1 at –100ŻC) and neopentane (Ň 0.07 at –108ŻC) to [Cp*Rh(CO)]. While the observation of both normal and inverse equilibrium isotope effects for coordination of alkanes to metal centers is counterintuitive, a simple rationalization is provided by the above calculations on {[H2Si(C5H4)2]W}.
3.
Equilibrium Isotope Effect for Oxidative Addition of Methane to [H2Si(C5H4)2]W(Me)H
In marked contrast to the EIE for coordination of methane which approaches zero at low temperature, the corresponding EIE for oxidative addition of methane to {[H2Si(C5H4)2]W} is normal at all temperatures and actually approaches infinity at low temperature.
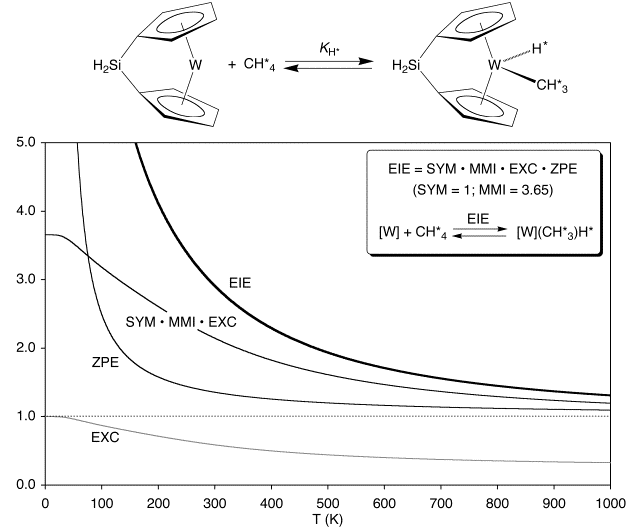
This dramatic difference between coordination and oxidative addition of methane is associated with the ZPE terms. Specifically, the ZPE term for coordination of methane is inverse at all temperatures (and zero at 0 K), while that for oxidative addition is normal at all temperatures (and infinity at 0 K).
While the total number of isotope sensitive vibrations
are the same for both [H2Si(C5H4)2]W(s–HMe) and [H2Si(C5H4)2]W(Me)H,
the principal difference in the ZPE term is a consequence of the fact that the
isotopically sensitive vibrations associated with the W–H bond of the
methyl hydride complex [H2Si(C5H4)2]W(Me)H,
namely a W–H stretch and two bends, are
of sufficiently low energy that they do not counter those associated with the
C–H bond that has that has been broken. As a result, the ZPE term for oxidative addition of the
C–H bond is normal
Selected References
“Applications of Deuterium Isotope Effects for Probing Aspects of Reactions Involving Oxidative Addition and Reductive Elimination of H–H and C–H Bonds.” Gerard Parkin J. Labelled Compounds and Radiopharmaceuticals 2007, 50, 1088-1114.
“A Normal Equilibrium Isotope Effect For Oxidative Addition of H2 to (h6–Anthracene)Mo(PMe3)3.” Guang Zhu, Kevin E. Janak and Gerard Parkin Chem. Commun. 2006, 2501-2503.
“Intramolecular N–H•••S Hydrogen Bonding in the Zinc Thiolate Complex [TmPh]ZnSCH2C(O)NHPh: A Mechanistic Investigation of Thiolate Alkylation as Probed by Kinetics Studies and by Kinetic Isotope Effects.” Melissa M. Morlok, Kevin E. Janak, Guang Zhu, Duncan A. Quarless, and Gerard Parkin J. Am. Chem. Soc. 2005, 127, 14039-14050.
“Molybdenocene Trihydride Complexes: Influence of a [Me2Si] Ansa Bridge on Classical versus Nonclassical Nature, Stability with Respect to Elimination of Dihydrogen, and Acidity.” Kevin E. Janak, Jun Ho Shin, and Gerard Parkin J. Am. Chem. Soc. 2004, 126, 13054-13070.
“Kinetic and Equilibrium Deuterium Isotope Effects for C–H Bond Reductive Elimination and Oxidative Addition Reactions Involving the Ansa–Tungstenocene Methyl–Hydride Complex [Me2Si(C5Me4)2]W(Me)H.” Kevin E. Janak, David G. Churchill, and Gerard Parkin in Activation and Functionalization of C–H Bonds, ACS Symposium Series 2004, 885, 86-104.
“Experimental Evidence for a Temperature Dependent Transition between Normal and Inverse Equilibrium Isotope Effects For Oxidative Addition of H2 to Ir(PMe2Ph)2(CO)Cl.” Kevin E. Janak and Gerard Parkin J. Am. Chem. Soc. 2003, 125, 13219-13224.
“Deuterium and Tritium Equilibrium Isotope Effects for Coordination and Oxidative Addition of Dihydrogen to [W(CO)5] and for the Interconversion of W(CO)5(h2–H2) and W(CO)5H2.” Kevin E. Janak and Gerard Parkin Organometallics 2003, 22, 4378-4380.
“Temperature Dependent Transitions between Normal and Inverse Equilibrium Isotope Effects For Coordination and Oxidative Addition of C–H and H–H Bonds to a Transition Metal Center.” Kevin E. Janak and Gerard Parkin J. Am. Chem. Soc. 2003, 125, 6889-6891.
“Normal and Inverse Primary Kinetic Deuterium Isotope Effects for C–H Bond Reductive Elimination and Oxidative Addition Reactions of Molybdenocene and Tungstenocene Complexes: Evidence for Benzene s–Complex Intermediates.” David G. Churchill, Kevin E. Janak, Joshua S. Wittenberg and Gerard Parkin J. Am. Chem. Soc. 2003, 125, 1403-1420.
“Computational Evidence that the Inverse Kinetic Isotope Effect for Reductive Elimination of Methane from a Tungstenocene Methyl–Hydride Complex is associated with the Inverse Equilibrium Isotope Effect for formation of a s–Complex Intermediate.” Kevin E. Janak, David G. Churchill, and Gerard Parkin Chem. Commun. 2003, 22-23.
“A Mechanistic and Theoretical Analysis of the Oxidative Addition of H2 to the Six-Coordinate Molybdenum and Tungsten Complexes, M(PMe3)4X2 (M = Mo, W; X = F, Cl, Br, I): An Inverse Equilibrium Isotope Effect and an Unprecedented Halide Dependence.” Tony Hascall, Daniel Rabinovich, Vincent J. Murphy, Michael D. Beachy, Richard A. Friesner, and Gerard Parkin J. Am. Chem. Soc. 1999, 121, 11402-11417.
“A Mechanistic Study of the Oxidative‑Addition of H2 to W(PMe3)4I2: Observation of an Inverse Equilibrium Isotope Effect.” Daniel Rabinovich and Gerard Parkin J. Am. Chem. Soc. 1993, 115, 353-354.
|
|||
