Publications with Peter W. Glynn

Peter Glynn and I have very similar backgrounds - only shifted in time by a few (too many) years. After studying mathematics at Carleton University in Ottawa, and doing an honors project on diffusion approximations for queues with Donald Dawson, Peter pursued graduate study in operations research at Stanford University. At Stanford Peter wrote his thesis on simulation output analysis for general-state-space Markov chains, earning his Ph.D. in 1982. Like me, Peter's dissertation advisor was Donald Iglehart. After teaching at Wisconsin for five years, Peter returned to Stanford to be on the faculty, where he is today.

My interactions with Peter began shortly after he finished his thesis. At a conference he said that he had some ideas about generalizing the famous conservation law L = 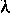W, also known as Little's law, and applying the results to simulation. I must have shown some flicker of recognition and appreciation. In turn, no good deed should go unpunished. Since there was a certain amount of devil in the details, that kept us both busy for quite a while. And one thing leads to another, as you can see below.

The focus of my research with Peter has been on asymptotics (primarily functional central limit theorems) that provide useful insight into queueing performance, conservation laws such as L = 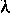W and ways to perform stochastic simulations more efficiently. There is an interesting excursion into hydrodynamic limits, stemming from our both being readers of Raj Srinivasan's Ph.D. thesis with Don Dawson at Carleton.

  1. A Central-Limit-Theorem Version of L = W. Queueing Systems: Theory and Applications, vol. 1, No. 2, September 1986, pp. 191-215. [published PDF]
  2. Sufficient Conditions for Functional Limit Theorem Versions of L = W. Queueing Systems: Theory and Applications, vol. 1, No. 3, 1987, pp. 279-287. [published PDF]
  3. Ordinary CLT and WLLN Versions of L = W. Mathematics of Operations Research, vol. 13, No. 4, 1988, pp. 674-692. [published PDF]
  4. An LIL Version of L = W. Mathematics of Operations Research, vol. 13, No. 4, 1988, pp. 693-710. [published PDF]
  5. Indirect Estimation Via L = W. Operations Research, vol. 37, No. 1, 1989, pp. 82-103. [published PDF]
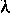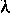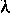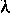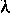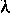  6. Extensions of the Queueing Relations L = W and H = 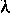G. Operations Research, vol. 37, No. 4, 1989, pp. 634-644. [published PDF]
  7. A New View of the Heavy-Traffic Limit for Infinite-Server Queues. Advances in Applied Probability, vol. 23, No. 1, 1991, pp. 188-209. [published PDF]
  8. Departures from Many Queues in Series. Annals of Applied Probability, vol. 1, No. 4, 1991, pp. 546-572. [published PDF]
  9. Estimating the Asymptotic Variance with Batch Means. Operations Research Letters, vol. 10, 1991, pp. 431-435. [PostScript] [PDF]
  10. The Asymptotic Validity of Sequential Stopping Rules in Stochastic Simulations. Annals of Applied Probability, vol. 2, No. 1, 1992, pp. 180-198. [published PDF]
  11. The Asymptotic Efficiency of Simulation Estimators. Operations Research, vol. 40, No. 3, 1992, pp. 505-520. [published PDF]
  12. Estimating Customer and Time Averages. Operations Research, vol. 41, No. 2, 1993, pp. 400-408 (with Benjamin Melamed). [published PDF]
  13. Limit Theorems for Cumulative Processes. Stochastic Processes and Their Applications, vol. 47, 1993, pp. 299-314. [published PDF]
  14. Logarithmic Asymptotics for Steady-State Tail Probabilities in a Single-Server Queue. Studies in Applied Probability, Papers in Honour of Lajos Takàcs, J. Galambos and J. Gani (eds.), Applied Probability Trust, Sheffield, England, 1994, pp. 131-156. [published PDF]
  15. Large Deviations Behavior of Counting Processes and Their Inverses. Queueing Systems, vol. 17, 1994, pp. 107-128. [published PDF]
  16. Heavy-Traffic Extreme-Value Limits for Queues. Operations Research Letters, vol. 18, 1995, pp. 107-111. [PDF] [published PDF]
  17. Winning the Hand of the Princess Saralinda. Appied Probability and Stochastic Processes, Festschrift for Julian Keilson, J. G. Shanthikumar and U. Sumita (eds.), Kluwer, Boston, 1999, Chapter 16, pp. 231-246 [PostScript] [PDF]
  18. Necessary Conditions in Limit Theorems for Cumulative Processes. Stochastic Processes and Their Applications, 2002, to appear. [published PDF]